Logarithmic Functions

A Logarithmic Function is an inverse function of an exponential function.

$f(x)=\log _{b}x$ and $g(x)=\ln x$

Logarithmic functions are widely used to represent quantities that spread out over a wide range (earthquake magnitude, sound level, etc).

Taking the logarithm of a number produces the exponent to which the base of the logarithm was originally raised.

Let’s go over how to graph logarithmic functions and how to solve logarithmic equations.

Graphing Logarithmic Functions

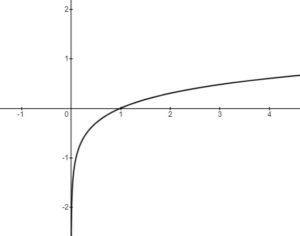
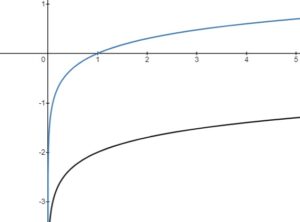
$f(x)=logx$ (base 10, from $g(x)=10^x$ )

$x$	$y$
-1	undefined
0	undefined
1	0
2	0.3
3	0.477

There are no $y$ -intercept, as there is a Vertical Asymptote (VA) at $x=0$

The $x$ -intercept is at (1,0)

Domain: { $x \epsilon R | x>0$ }

Range: { $y\epsilon R$ }

$f(x)=lnx$ (base $e$ , natural logarithm from $g(x)=e^x$ )

$x$	$y$
-1	undefined
0	undefined
1	0
2	0.693
3	1.0986

There are no $y$ -intercept, as there is a Vertical Asymptote (VA) at $x=0$

The $x$ -intercept is at (1,0)

Domain: { $y\epsilon R$ }

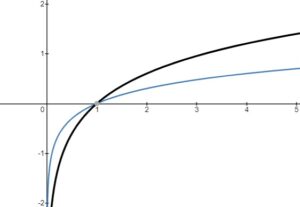
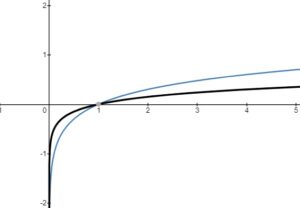
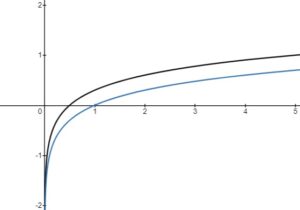
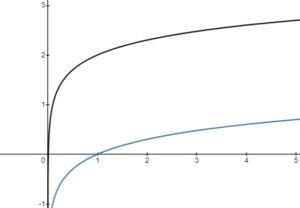
Transformations of Log Functions

$f(x)=alog(k(x-c))+d$

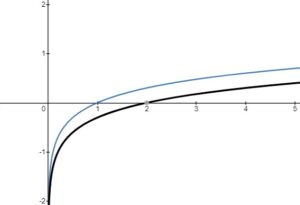
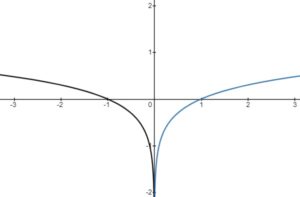
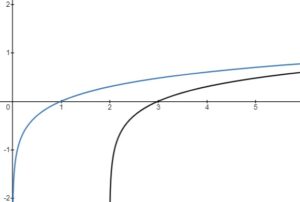
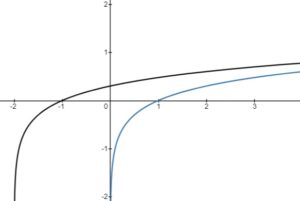
$a$ – vertical stretch or compression, reflection in the $x$ -axis

$k$ – horizontal stretch or compression, reflection in the $y$ -axis

$c$ – horizontal translation left or right

$d$ – vertical translation up or down

$f(x)=2logx$	$f(x)=\frac{1}{2}logx$

$f(x)=log2x$	$f(x)=log\frac{1}{2}x$

$f(x)=-logx$	$f(x)=log(-x)$

$f(x)=log(x-2)$	$f(x)=log(x+2)$

$f(x)=logx-2$	$f(x)=logx+2$

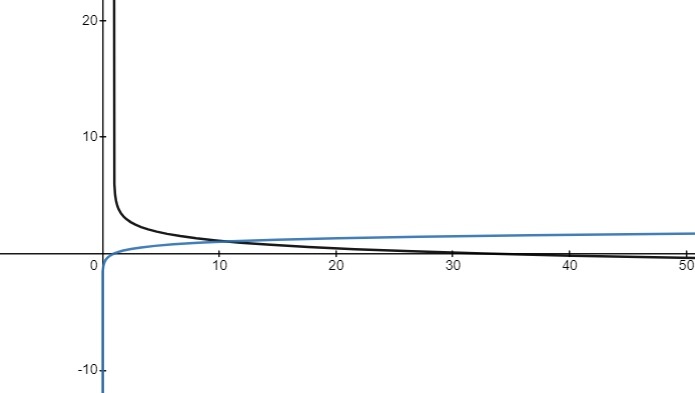
State transformations in order and graph

$f(x)=-2log(x-1)+3$

vertical compression by a factor of 2
reflection in the $x$ – axis
horizontal translation 1 unit left
vertical translation 3 units up

Vertical Asymptote (VA): $x=1$

$y$ – intercept: $f(0)=-2log(0-1)+3$ – NONE

$x$ – intercept(s):

In order to determine the $x$ – intercepts, set the equation to = 0, then solve it for $x$ by performing inverse operations in the reverse BEDMAS order.

At the end, the equation would need to be changed to an exponential form in order to be solved.

$0=-2log(x-1)+3$

$-3=-2log(x-1)$

$\frac{-3}{-2}=log(x-1)$

$\frac{3}{2}=log(x-1)$

at this point, in order to solve this equation, represent it in its exponential form, where base is 10 and the exponent is $\frac{3}{2}$ :

$10^{\frac{3}{2}}=x-1$

$x=10^\frac{3}{2}+1$

$x=32.6$

Therefore, the $x$ – intercept is at (32.6, 0)

Review Exponential Functions

Applications of Logs

Log laws (base 10 logarithm)

$loga + log b = log(ab)$

$loga - logb=log (\frac{a}{b})$

$loga^b=bloga$

$log1=0$

Laws of Logarithms Quiz

Example 1: A new car is purchased for $20,000. The car’s value after $t$ years is given by $V=20,000(0.8)^t$ . How long will it take for the car to be worth half of its purchase value?

Solution:

$10,000=20,000(0.8)^t$

$\frac{10,000}{20,000}=0.8^t$

$0.5=0.8^t$ convert into logarithmic form

$log0.5=tlog0.8$

$t=\frac{log0.5}{log0.8}$

$t=3.1$

Therefore, it would take just over 3 years for the car do depreciate to half of its original value.

Example 2: On the Richter scale, the magnitude of the earthquake in City A is 2.7 and the magnitude of the earthquake in City $B$ is $1.3$ . How many times stronger is the earthquake in City A?

Formula to compare two earthquakes: $M_{2}-M_{1}=log(\frac{I_{2}}{I_{1}})$ where M is the magnitude and I is the intensity.