Jump discontinuity, a term that might seem complex at first glance, holds significant importance in the realm of mathematics, particularly within the study of functions. It’s a predictive marker that mathematicians and students alike grapple with to understand and analyze the behavior of functions. The presence of a jump discontinuity indicates a sudden leap in the value of the function at a certain point, making the function non-continuous at that exact spot. It represents a fascinating aspect of mathematical analysis, emphasizing why a thorough grasp of continuous and non-continuous functions is crucial for solving real-world problems.
This article delves into the concept of jump discontinuity, providing a foundation for identifying and analyzing these critical points within functions. It begins by unpacking the nature of jump discontinuities, offering a clear definition and distinguishing them from other types of discontinuities. Following this, readers will be guided through practical examples of jump discontinuities, showcasing how they can be spotted and interpreted in various mathematical functions. Additionally, the article will explore the impact of jump discontinuities on the overall behavior of functions, providing insights into their theoretical and practical significance. Through this journey, the article aims to equip readers with the knowledge to not only recognize but also effectively analyze jump discontinuities, enhancing their comprehension of mathematical continuity and its implications.
Understanding Jump Discontinuities in Functions
Definition and Basic Concepts
A jump discontinuity in a function occurs when there is a sudden change in the function’s value at a specific point, with no intermediate values connecting these different points. This type of discontinuity is characterized by the existence of left-hand and right-hand limits at a point, which are not equal to each other. Specifically, for a function (f(x)) at (x=p), a jump discontinuity is present if the limit of (f(x)) as (x) approaches (p) from the left is (A), and the limit as (x) approaches (p) from the right is (B), where (A) and (B) are real numbers but (A \neq B) [4]. This definition highlights the primary feature of jump discontinuities: the existence of two distinct, non-equal limits at a single point in the function’s domain. It is essential to understand that simply observing a ‘jump’ on a graph is not sufficient to confirm a jump discontinuity; one must analyze the left-hand and right-hand limits to make this determination [4][5].
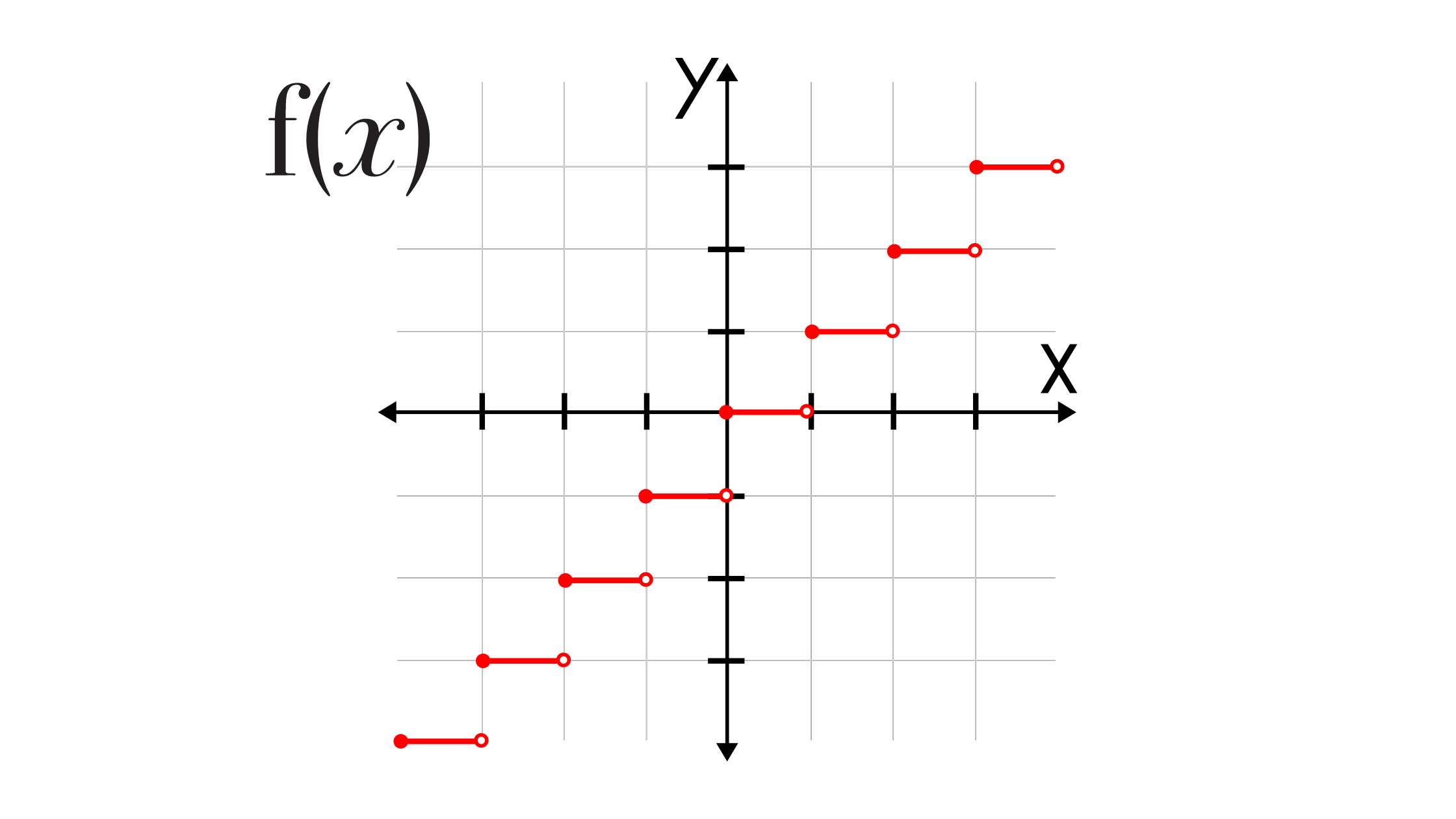
Visualizing with Graphs
Graphically, a jump discontinuity is represented by a ‘gap’ or ‘break’ in the graph of the function at the discontinuity point. This visual break indicates that the function values abruptly change from one point to another without passing through intermediate values [5][7]. To effectively graph a jump discontinuity, one should follow specific steps: Identify a function with a jump discontinuity, determine the values on both sides of the discontinuity, plot points to represent the function’s behavior around the discontinuity, and connect these points with a vertical line segment. This segment visually represents the discontinuity, and depending on the convention, open or filled circles may be used at the ends of the line segment to indicate the function’s behavior at the discontinuity point [8]. This visual approach not only aids in identifying jump discontinuities but also provides insight into the function’s overall behavior and how such discontinuities impact the function’s properties [5][7].
Exploring Examples of Jump Discontinuities
Piecewise Functions
Piecewise functions, defined by different formulas or expressions over various intervals, are a common source of jump discontinuities. These discontinuities occur at points where the function’s definition changes, leading to a ‘jump’ from one value to another without intermediate values. For example, a piecewise function might be defined one way for (x < 0) and another for (x \geq 0), with a jump discontinuity at (x = 0) where the function’s value suddenly changes. Understanding the domain restrictions and evaluating the function within these domains is crucial for correctly identifying and analyzing these jumps [10][11].
Real-World Applications
Jump discontinuities are not just mathematical curiosities; they have significant implications in real-world scenarios across various fields such as economics, physics, and engineering. For instance, the demand for a product might show a jump discontinuity when there is an abrupt price change, reflecting a sudden shift in consumer behavior. Similarly, in electrical engineering, the voltage across a circuit component can exhibit a jump discontinuity when the component switches state, impacting the circuit’s overall behavior. These examples highlight the importance of recognizing and understanding jump discontinuities in practical applications [10][14].
Analyzing the Impact of Jump Discontinuities
On Limit Calculations
Jump discontinuities significantly affect limit calculations, as they can lead to situations where the limit of a function as it approaches a point of discontinuity does not exist or may have different values depending on the direction of approach. This inconsistency in limits is crucial in fields such as physics, engineering, and economics, where precise mathematical models are employed to describe and predict real-world phenomena. The inability to determine a single limit value at points of jump discontinuity necessitates a deeper analysis and understanding of the function’s behavior, which is essential for accurate mathematical modeling and analysis [19][20][16][17].
In Mathematical Modeling
In mathematical modeling, jump discontinuities present a challenge, as they represent a departure from the idealized smooth behavior often assumed in physical systems. Real-world phenomena, when closely examined, reveal that what may be modeled as a jump discontinuity is, in reality, a rapid but continuous change. This discrepancy between the mathematical model and physical reality can lead to significant errors in numerical modeling, affecting the accuracy of predictions and simulations. For instance, modeling a physical object’s sharp edges or a sudden change in acceleration can introduce errors, as these do not perfectly represent the gradual transitions found in nature. Thus, understanding the impact of jump discontinuities and incorporating methods to address them in mathematical models is crucial for achieving more accurate and reliable results in various scientific and engineering applications [20].
Conclusion
Throughout the exploration of jump discontinuities in functions, we have navigated the intricate landscape from their fundamental definitions to real-world implications, emphasizing the importance of recognizing and analyzing these discontinuities. By delving into practical examples and mathematical models, the article has illuminated the critical role that understanding jump discontinuities plays in various fields, including physics, engineering, and economics. This journey not only enhances our comprehension of mathematical functions but also underscores the significance of accurate modeling and analysis in solving complex real-world problems.
As we conclude, it’s evident that the capability to identify and analyze jump discontinuities extends beyond academic intrigue, offering substantial benefits in practical applications and theoretical understanding. This analysis invites further research and discussion, encouraging a deeper dive into the nuances of discontinuities and their modeling. Acknowledging the challenges and opportunities presented by jump discontinuities paves the way for advancements in mathematical analysis and its applications, highlighting the ever-evolving relationship between abstract mathematical concepts and their tangible impacts on the real world.
FAQs
How Can You Detect a Jump Discontinuity in a Function?
To identify a jump discontinuity, examine the function at points where the left- and right-hand limits do not match, which is common in piecewise functions. By comparing the limits from both sides at each potential point of discontinuity, you can determine whether the function exhibits continuous behavior or a jump discontinuity.
What Steps Should You Take to Find a Function’s Discontinuity?
To find a function’s discontinuity, begin by factoring both the numerator and the denominator of the function. A discontinuity occurs at a point where a value causes both the numerator and denominator to equal zero. Identifying such values will help you pinpoint where discontinuities lie.
How Can Discontinuities Be Spotted on a Graph?
Discontinuities on a graph can be identified by looking for open and closed circles or by noticing vertical asymptotes, which are represented by dashed lines. These visual cues on a graph, along with zero values in the denominator when working with formulas, signal points of discontinuity.
What Defines a Jump Discontinuity Mathematically?
A jump discontinuity in a function is defined mathematically when the limit of the function as x approaches a point p from the right is A, and the limit as x approaches p from the left is B, with A and B being distinct real numbers (A ≠ B). The Heaviside or unit step function serves as a classic example of a function that demonstrates a jump discontinuity.
Also read Functions and Discontinuities
References
[1] – https://study.com/academy/lesson/jump-discontinuities-definition-lesson-quiz.html
[2] – https://study.com/skill/learn/how-to-find-jump-discontinuities-explanation.html
[3] – https://www.studysmarter.co.uk/explanations/math/calculus/jump-discontinuity/
[4] – https://www.vaia.com/en-us/explanations/math/calculus/jump-discontinuity/
[5] – https://study.com/academy/lesson/jump-discontinuities-definition-lesson-quiz.html
[6] – https://mathworld.wolfram.com/JumpDiscontinuity.html
[7] – https://study.com/skill/learn/how-to-find-jump-discontinuities-explanation.html
[8] – https://www.ck12.org/flexi/precalculus/excluded-values-for-rational-expressions/how-to-graph-a-jump-discontinuity/
[9] – https://www.khanacademy.org/math/ap-calculus-ab/ab-limits-new/ab-1-10/v/types-of-discontinuities
[10] – https://study.com/academy/lesson/jump-discontinuities-definition-lesson-quiz.html
[11] – https://www.youtube.com/watch?v=jr0Xw8jxZT0
[12] – https://socratic.org/questions/how-do-you-find-discontinuity-of-a-piecewise-function
[13] – https://www.freemathhelp.com/forum/threads/real-world-applications.66784/
[14] – https://www.geeksforgeeks.org/real-life-applications-of-discontinuity/
[15] – https://www.physicsforums.com/threads/exploring-jumps-discontinuities-in-real-world-equations.559413/
[16] – https://magoosh.com/hs/ap/ap-calculus-review-discontinuities/
[17] – https://www.khanacademy.org/math/ap-calculus-ab/ab-limits-new/ab-1-10/v/types-of-discontinuities
[18] – https://study.com/skill/learn/how-to-find-jump-discontinuities-explanation.html
[19] – https://study.com/academy/lesson/jump-discontinuities-definition-lesson-quiz.html
[20] – https://www.physicsforums.com/threads/exploring-jumps-discontinuities-in-real-world-equations.559413/
[22] – https://deepai.org/machine-learning-glossary-and-terms/jump-discontinuity
[23] – https://study.com/skill/learn/how-to-find-jump-discontinuities-explanation.html
[24] – https://math.libretexts.org/Courses/Monroe_Community_College/MTH_210_Calculus_I_(Professor_Dean)/Chapter_2_Limits/2.6%3A_Continuity
There are no comments yet