Exponential Functions. Transformations and Applications
Exponential functions are functions that model a very rapid growth or a very rapid decay of something. They are used to calculate finances, bacteria populations, the amount of chemical substance and much more.
In the exponential function the input is in the exponent. The base of the power determines whether the relation is a growth or a decay.
The graph of an exponential function is a curve that in a parent function form approaches, but never touches or crosses the x-axis. Thus, there is a horizontal asymptote of y = 0.
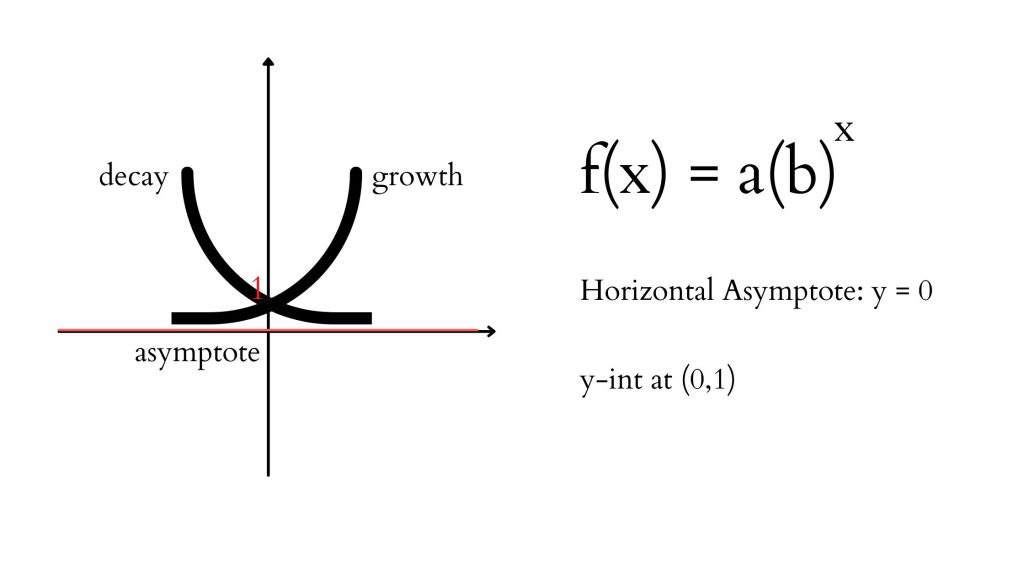
The horizontal asymptote exists because no positive base to any power (positive or negative) will result in a 0 or a negative output (for example, no matter what exponent you raise the base of 4 to, the result will never be 0 or something negative).
This also means that there will be a restriction on the range of the function (as the function is undefined at or below 0). This may change when you transform the function and add a reflection and/or vertical translation. There are no restrictions on the domain of the exponential function.
Transformations of Exponential Functions
Just like any other type of function, an exponential function can be transformed. It can be reflected, stretched and compressed, as well as shifted vertically and horizontally.
The general equation of an exponential function depicting transformations is the following:
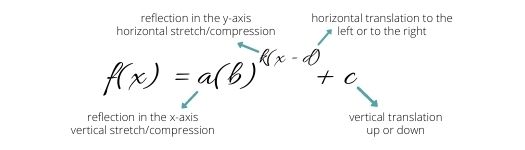
- When a is negative, the function is reflected in the x-axis (affects the range of the function)
- When k is negative, the function is reflected in the y-axis
- When a is greater than 1, the function is vertically stretched
- When a is greater than 0 and less than 1, the function is vertically compressed
- When k is greater than 1, the function is horizontally compressed
- When k is greater than 0 and less than 1, the function is horizontally stretched
- When d is positive, move right; when d is negative, move left (opposite sign in brackets)
- When c is positive, move up; when c is negative, move down (affects the location of the horizontal asymptote)
Exponential Growth and Decay Word Problems
In real life exponential functions represent rapid growth and decay.
Watch how to solve word problem involving exponential growth and decay:
Another type of exponential function applications involves doubling period and half life. Watch how to solve doubling period and half life problems, including how to solve for an exponent: