Rational Functions

A Rational Function is a function given as a ratio of two polynomial functions. The denominator cannot be 0.

$f(x)=\frac{P(x)}{Q(x)}$ where $Q(x)\neq 0$

We are going to consider three scenarios of the rational function equations and their characteristics:

The expression in the numerator has a lower degree than the expression in the denominator
The expressions in the numerator and in the denominator have the same degree
The expression in the numerator is 1 degree higher than the expression in the denominator

Rational Functions: Degree of Numerator < Degree of Denominator

$f(x)=\frac{1}{x-3}$

The above function has the following characteristics:

The equation of the Vertical Asymptote (VA) is $x=3$ , since this value will make the denominator $=0$ , which will make the function undefined.

The equation of the Horizontal Asymptote (HA) is $y=0$ , since the degree of the numerator is < than the degree of the denominator. Algebraically it comes from trying to determine the roots: $0=\frac{1}{x-3}$ . Since the equation has no solutions, there are no roots and the function has a horizontal asymptote.

There are no roots ( $x$ -intercepts) – see above

The $y$ -intercept is at $(0,-\frac{1}{3})$ , which can be determined from the equation by dividing the constants or by substituting 0 for $x$ in the equation and evaluating $f(0)$ .

Domain is { $x\epsilon R|x\neq 3$ }; Range is { $y\epsilon R|y\neq 0$ }

$g(x)=\frac{x-2}{x^2+2x-15}$

The above function has the following characteristics:

The equations of the Vertical Asymptotes (VAs) are $x=3$ and $x=-5$ , since $x^2+2x-15$ needs to be factored in order to determine the values that would make the denominator 0.

The equation of the Horizontal Asymptote (HA) is $y=0$ , since the degree of the numerator is < than the degree of the denominator. Algebraically it comes from trying to determine the roots: $0=\frac{x-2}{x^2+2x-15}$ ; $0\neq x-2$ Since the equation has no solutions, there are no roots and the function has a horizontal asymptote.

There are no roots ( $x$ -intercepts) – see above

The $y$ -intercept is at $(0,\frac{2}{15})$ , which can be determined from the equation by dividing the constants or by substituting 0 for $x$ in the equation and evaluating $f(0)$ .

Domain is { $x\epsilon R|x\neq -5,3$ }; Range is { $y\epsilon R|y\neq 0$ }

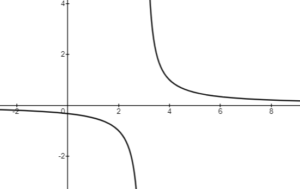
Rational Functions: Degree of Numerator = Degree of Denominator

$f(x)=\frac{2x-3}{3x+9}$

The above function has the following characteristics:

The equations of a Vertical Asymptote (VA) is $x=-3$ , since if we set $3x+9=0$ and solve for $x$ , the value that would make the denominator 0 would be $-3$ .

The equation of the Horizontal Asymptote (HA) is $y=\frac{2}{3}$ , since the degree of the numerator is = to the degree of the denominator. The equation of the HA is always equal to the ratio of the leading coefficients in the numerator and in the denominator when the expressions in the numerator and the denominator are the same.

In order to determine roots (x-intercepts), set the numerator to = 0 and solve for $x$ : $2x-3=0$ ; so the x-intercept is at $(\frac{3}{2},0)$ .

The $y$ -intercept is at $(0,-\frac{1}{3})$ , which can be determined from the equation by dividing the constants or by substituting 0 for $x$ in the equation and evaluating $f(0)$ .

Domain is { $x\epsilon R|x\neq -3$ }; Range is { $y\epsilon R|y\neq \frac{2}{3}$ }

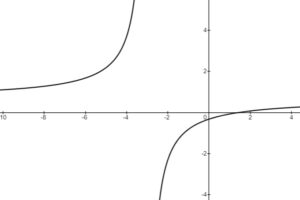
Rational Functions: Degree of Numerator 1 greater than Degree of Denominator

$f(x)=\frac{x^2-7x+10}{x-1}$

The above function has the following characteristics:

There is one Vertical Asymptote (VA) at $x=1$ , since this is the value that would make the denominator 0 and we cannot divide by 0.

Since the degree of the numerator is 1 greater than the degree of the denominator, there is no HA, but instead there is an Oblique (Slant) Asymptote (OA). In order to determine the equation of the OA, divide the polynomial in the numerator by the polynomial in the denominator. The quotient is the equation of the OA and the remainder can be ignored.

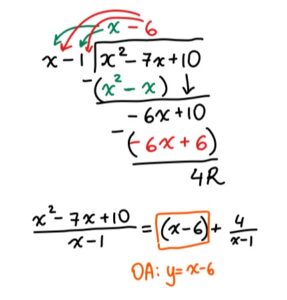
find OA

In order to determine the x-intercepts, set the expression in the numerator to = 0 and solve for $x$ . In the case of the given function, the numerator needs to be factored first: $(x-2)(x-5)=0$ . So the x-intercepts are $(2,0), (5,0)$ .

The $y$ -intercept is at $(0,-10)$ , which can be determined from the equation by dividing the constants or by substituting 0 for $x$ in the equation and evaluating $f(0)$ .

Rational Functions: Holes

$g(x)=\frac{x^2+5x+6}{x+3}$

When the equation of a rational function can be factored, it needs to be factored before determining the components of the function.

This is because sometimes some factors may be reduced and eliminated completely, creating a hole at a particular point, which would be a restriction at only one point, rather than the asymptote.

If we factor the function above, we would get the following:

$g(x)=\frac{(x+2)(x+3)}{x+3}$

As you can see, there are two identical factors in the numerator and in the denominator that could be reduced completely (none would remain in the expression). Thus, there is no Vertical Asymptote, but rather a hole.

Holes only occur at specific points if a factor is eliminated completely. If not, then that factor could still be an asymptote (if it remains in the denominator) or an x-intercept (if it remains in the numerator).

So, in the simplified form, the equation of $g(x)=\frac{x^2+5x+6}{x+3}$ would look like $g(x)=x+2$ with a hole at $x=-3$ .

Since a hole is not an asymptote, but rather a point with a set of coordinates, the corresponding y-coordinate needs to be determined for the established x-coordinate using the simplified equation:

$g(-3)=-3+2$

$g(-3)=-1$

Therefore, the hole occurs at $(-3,-1)$ on the function $g(x)=x+2$ and the function will be undefined at that point as the value of $-1$ will be approached very closely but not defined.

The Domain and Range of the function would be

D: { $x\epsilon R | x\neq -3$ }; R: { $y\epsilon R | y\neq -1$ }

Rational Functions: End Behaviour and Behaviour Around Asymptotes

Horizontal and Vertical Asymptotes

As $x \rightarrow \pm \infty$ , then $y\rightarrow$ Horizontal Asymptote (HA)
Test the x-values on both sides of the Vertical Asymptotes (VAs) in order to establish how the function behaves around them – substitute the x-coordinates to get the corresponding y-coordinates and plot the points
There could be exceptional points where a Horizontal Asymptote could be crossed.

Oblique and Vertical Asymptotes

As $x \rightarrow \pm \infty$ , then $y\rightarrow$ Oblique Asymptote (OA) in the form $y=mx+b$
Test the x-values on both sides of the Vertical Asymptotes (VAs) in order to establish how the function behaves around them – substitute the x-coordinates to get the corresponding y-coordinates and plot the points
A function can only have either an HA or OA, but not both

Steps for Graphing Rational Functions

Record the equation of the function in both the expanded and the factored forms
Establish if there are any holes
State the equations of the Vertical Asymptotes
Determine the equation of a Horizontal Asymptote or an Oblique Asymptote
Determine the x-intercepts by setting the numerator = 0
Determine the y-intercept by determining the ratio of the constants or by substituting 0 for x and solving for y.
Determine the End Behaviour and Behaviour around the Asymptotes
Connect all points and pieces into smooth curves and clearly mark the asymptotes and holes