Polynomial Functions

A Polynomial function is a function in which the independent variable is a non-negative integer exponent.

An algebraic term with the highest exponent is the leading term that determines the degree of the function; its coefficient is the leading coefficient.

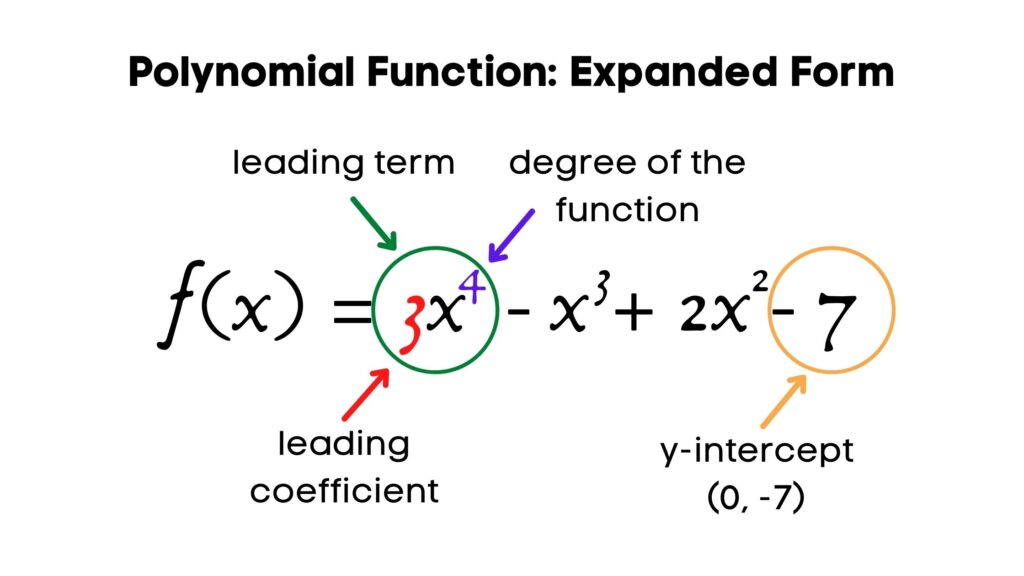
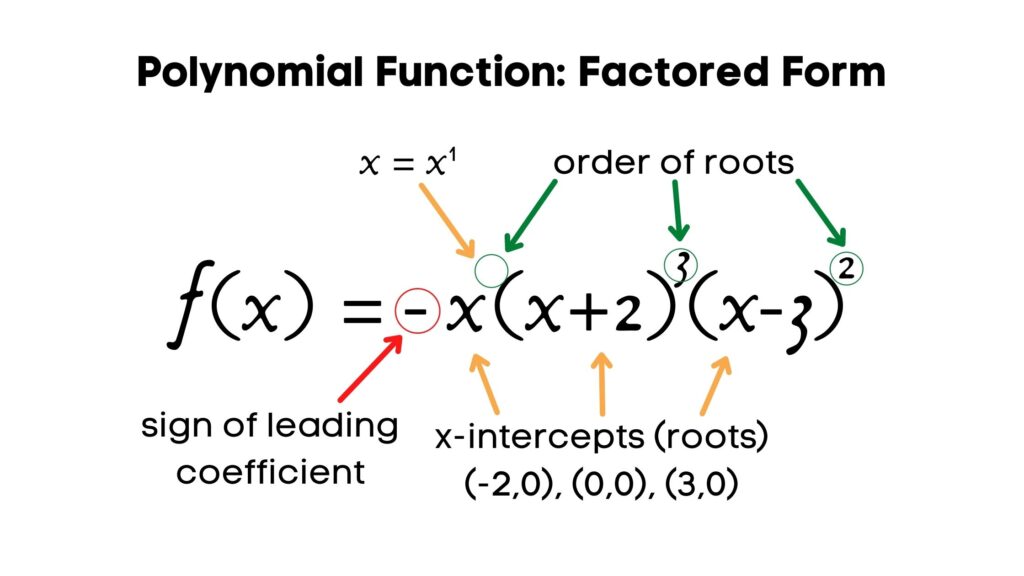
polynomial function factored form

Polynomial Functions: Characteristics and Graphs

A degree of a polynomial function = maximum number of x-intercepts.

A turning point is where a function changes from increasing to decreasing or vice versa.

The maximum number of turning points (local maximums and local minimums) = one less than the degree of a function.

The sign of the leading coefficient determines the end behaviour of a polynomial function:

  • Odd number degree + positive leading coefficient: Q3 – Q1
  • Odd number degree + negative leading coefficient: Q2 – Q4
  • Even number degree + positive leading coefficient: Q2 – Q1
  • Even number degree + negative leading coefficient: Q3 – Q4
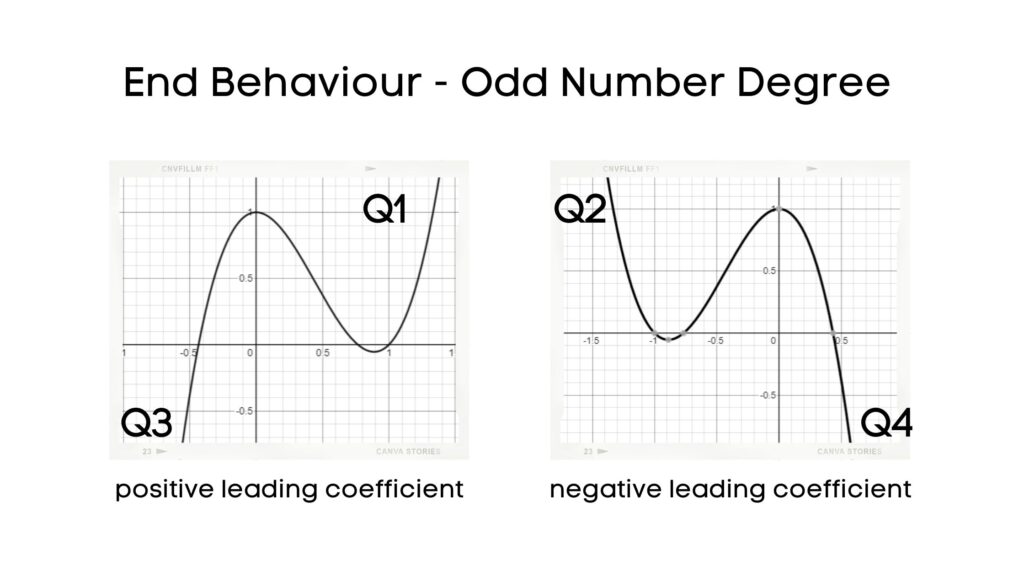
end behaviour odd number degree
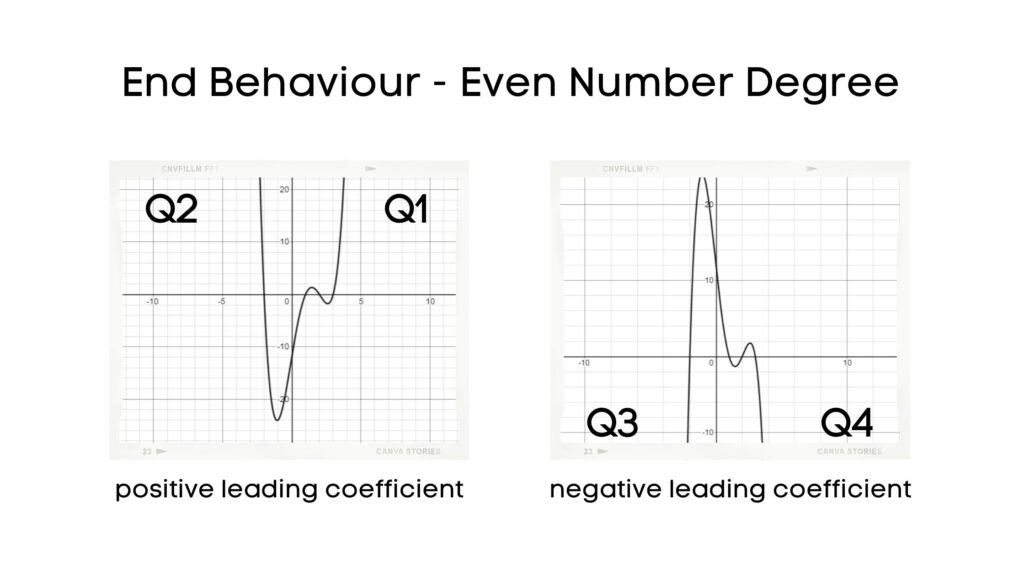
end behaviour even number degree

In the expanded form, the constant value = y-intercept of the function.

In the factored form, the factors help determine the x-intercepts (roots).

The order of x-intercepts (roots) is how many times that particular x-intercept is repeated.

If the x-intercept is of an even number order (2,4,6,…) – there is a bounce and a turning point at that x-intercept.

If the x-intercept is of an odd number order (1,3,5,…) – the graph curves through the x-intercept and there is no turning point at that x-intercept.

Polynomial Functions: Symmetry

Odd Function – odd symmetry – when a function is symmetrical about the origin (rotational symmetry).

Even Function – even symmetry – when a function is symmetrical about the y-axis (mirror symmetry).

Neither Even nor Odd Function – neither symmetrical about the origin nor about the y-axis.

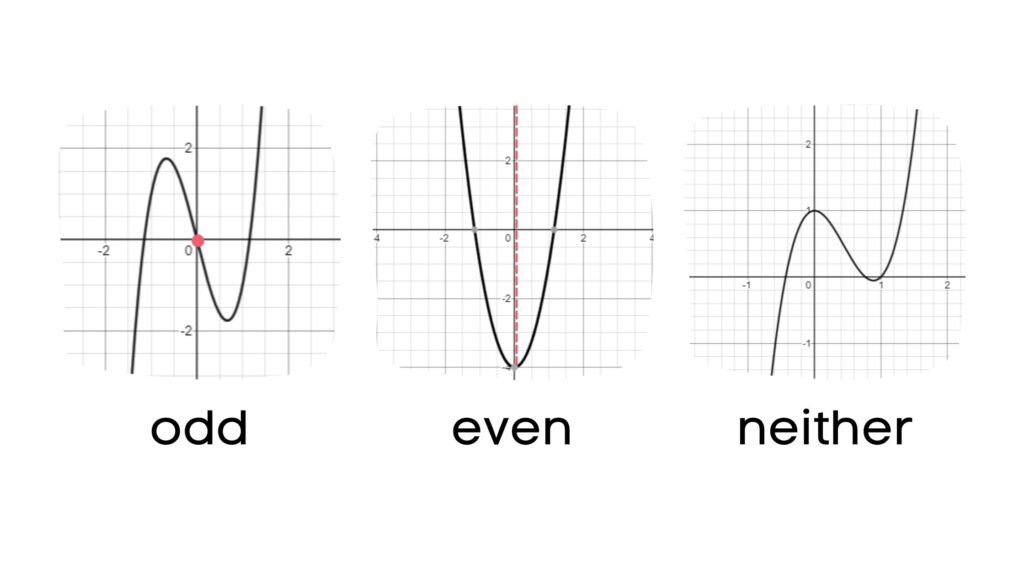
even and odd symmetry of polynomial function

It is also possible to determine the symmetry algebraically, by testing the equation of the function.

Given the equation of the function f(x), we can test f(-x) and see if every term changes the sign to the opposite or not.

 

For example, the function  f(x)=3x^3-x  is ODD, since

f(-x)=3(-x)^3-(-x) 

f(-x)=-3x^3+x

Every sign within the function equation has changed to the opposite.

 

The function  f(x)=2x^4-3x^2+1  is EVEN, since

f(-x)=2(-x)^4-3(-x)^2+1

f(-x)=2x^4-3x^2+1

Every sign within the function equation has remained unchanged.

 

The function  f(x)=3x^3-2x^2-15  is NEITHER, since

f(-x)=3(-x)^3-2(-x)^2-15

f(-x)=-3x^3-2x^2-15

The signs of some terms have changed and others – remained the same.

NOTE: It is important to differentiate between odd/even degree and odd/even symmetry – those are different concepts, even though similar terminology is used to describe them.

Check your understanding with Polynomial Functions Quiz and Even and Odd Symmetry Quiz