Calculus: Limits

A Limit of a function is the value the function approaches at a specific input. Limits help us determine whether a function is continuous or discontinuous, as well as how the function behaves over a certain domain.

\lim_{x\rightarrow a}(f(x))=f(a)

\lim_{x\rightarrow 3}(2x+1) = 7  means that when  x  gets closer to 3 from left and right, the value of  y  gets closer to 7.

Read it as: “the limit of  2x+1 as  x  approaches 3 is 7″

For continuous functions evaluating the limit is very similar to just evaluating the function at a certain value of the independent variable.

However, when it comes to discontinuous function, evaluating the limit may involve several situations that must be considered.

Evaluating Limits (Algebraic Limits)

Let’s consider different types of functions and learn how to evaluate a limit using the specific function equation.

Example 1: Linear Function

Evaluate the limit 

\lim_{x\rightarrow 3}(2x-4)

\lim_{x\rightarrow 3}(2x-4)=2(3)-4 = 6-4=2

\therefore \lim_{x\rightarrow 3}(2x-4)=2

Example 2: Quadratic Function

Evaluate the limit

\lim_{x\rightarrow -2}(-2x^2-3x+4)

\lim_{x\rightarrow -2}(-2x^2-3x+4)=-2(-2)^2-3(-2)+4=-2(4)+6+4=-8+10=2

\therefore \lim_{x\rightarrow -2}(-2x^2-3x+4)=2

Example 3: Exponential Function

Evaluate the limit

\lim_{x\rightarrow 2}(3(2)^x)

\lim_{x\rightarrow 2}(3(2)^x)=3(2)^2=3(4)=12

\therefore \lim_{x\rightarrow 2}(3(2)^x)=12

Example 4: Square Root Function

Evaluate the limit

\lim_{x\rightarrow 1}(2\sqrt{x-2})

\lim_{x\rightarrow 1}(2\sqrt{x-1})=2\sqrt{1-2} =  Limit Does Not Exist

This is because this function only exists at or past (to the right) of  x=2.

Example: Rational Function

Evaluate the limit

\lim_{x\rightarrow 5}\frac{x^2+2x-35}{x-5}

If we follow the previous examples, we would end up with the following:

\lim_{x\rightarrow 5}\frac{x^2+2x-35}{x-5}=\frac{5^2+2(5)-35}{5-5}   which results in  \frac{0}{0} 

We cannot divide by zero and the above result has no meaning.

Instead, always factor rational fractions first and simplify. Only then evaluate the limit using the simplified expression of the function:

\lim_{x\rightarrow 5}(\frac{(x-5)(x+7)}{(x-5)})   factors (x-5) will be reduced completely

\lim_{x\rightarrow 5}(x+7)=5+7=12

\therefore \lim_{x\rightarrow 5}(\frac{x^2+2x-35}{x-5})=12

The limit exists at x=5, but the function is undefined at that point, since x=5 is a restriction (a hole).

Limits from Graphs

Sometimes, you may be asked to determine the limit of a function given the graph of a function.

The limit can also be determined approaching the value of the input from the left and from the right separately.

Let’s consider the following graph of the function f(x):

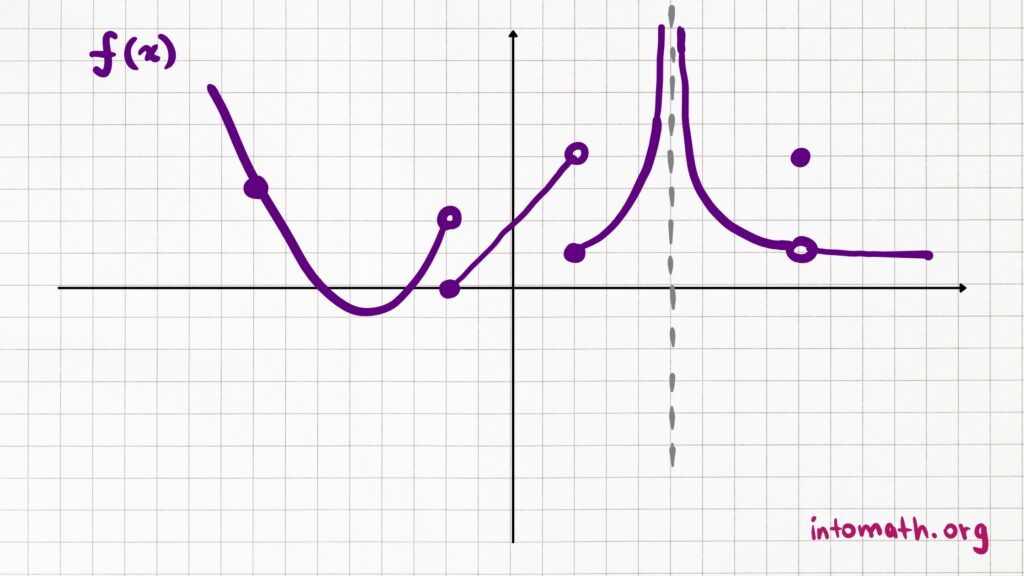
limits graph

Continuous:

\lim_{x\rightarrow -8}(f(x))=3  because the function is continuous and defined at  x=-8

Jump Discontinuity:

\lim_{x\rightarrow -2^-}(f(x))=2  because coming from the left at x=-2 the function approaches the value of  y=2

\lim_{x\rightarrow -2^+}(f(x))=0 because coming from the right at x=-2 the function takes on the value of y=0

\lim_{x\rightarrow -2}(f(x))=DNE   because in order for the limit to exist at a specific input, the output values coming from the left and from the right must be equal (at x=-2 the limits are result in different values coming from the left and from the right)

\lim_{x\rightarrow 2^-}(f(x))=4 because coming from the left at x=2 the function approaches the value of y=4

\lim_{x\rightarrow 2^+}(f(x))=1 because coming from the left at x=2 the function approaches the value of y=1

\lim_{x\rightarrow 2}(f(x))=DNE

Infinite Discontinuity: 

\lim_{x\rightarrow 5^-}(f(x))=\infty  since the function stretches along the vertical asymptote

\lim_{x\rightarrow 5^+}(f(x))=\infty since the function stretches along the vertical asymptote

\lim_{x\rightarrow 5}(f(x))=\infty since the function stretches along the vertical asymptote from both the left and the right and the value is the same for both limits

Removable (Point) Discontinuity:

\lim_{x\rightarrow 9}(f(x))=1  since 1 is the value the function approaches from the left and from the right at  x=9. 

However, the function is defined at  (9,4)

Practice by taking this FREE ONLINE LIMITS QUIZ