Unit Circle Trigonometry (Degrees)
Periodic phenomena or periodic nature of things are very common in our lives.
Think of a clock or a wave or even the change in seasons.
If we were to represent a periodic relationship we would create a circle and each new rotation would be the next time the same event occurs.
This brings us to the Unit Circle Trigonometry.
In fact, in mathematics this is exactly what we use to represent and define the period behaviour – a unit circle.
A unit circle is a circle with a radius of 1 unit. It shows the relationship of the angles around the circle, the radius and the vertical and horizontal distances.
Together, the vertical, the horizontal distances and the radius form a right angle triangle and depending on the angle at the center of the circle, the trigonometric ratios formed are different.
Travelling around the unit circle counterclockwise forms positive angles. Travelling around the unit circle clockwise forms negative angles.
CAST Rule
A unit circle is divided into quadrants.
In the first quadrant (Q1) all of the acute angles are located and we call them RELATED ACUTE ANGLES since the rest of the angles around the circle are based on RAAs and result in the same trig ratios, with the same or different signs.
The sign of the trig ratio of an angle depends on the Quadrant in which the angle is located.
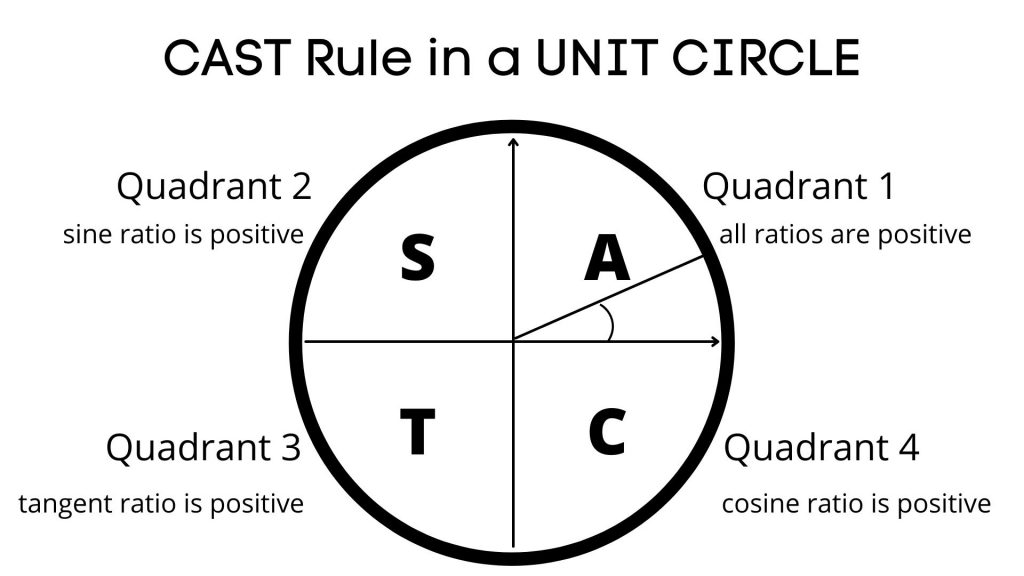
In Q1 ALL TRIG RATIOS ARE POSITIVE
In Q2 ONLY SINE RATIO IS POSITIVE
IN Q3 ONLY TANGENT RATIO IS POSITIVE
IN Q4 ONLY COSINE RATIO IS POSITIVE
We can use the CAST rule starting from Q4 to memorize the signs of the trig ratios.
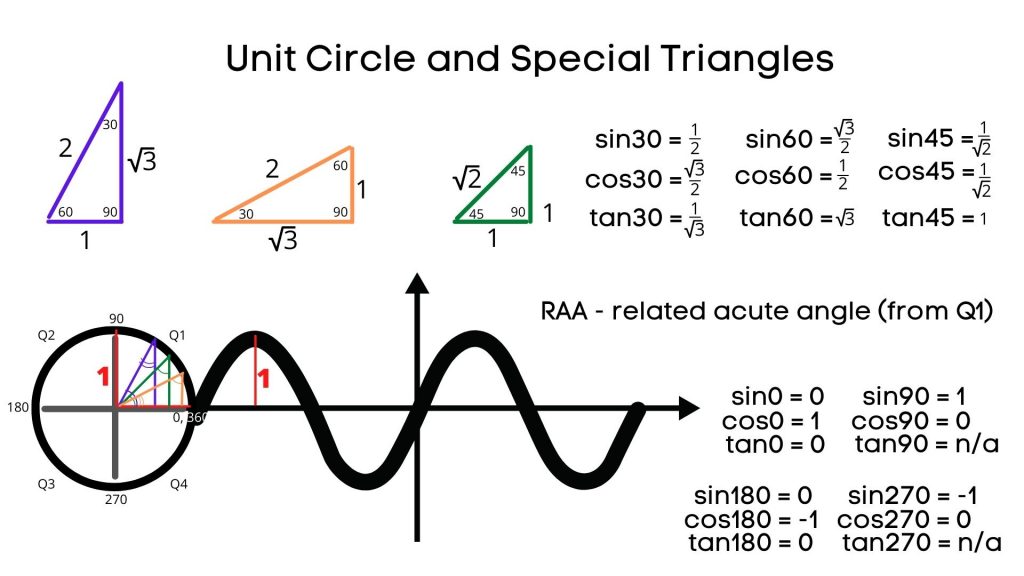
Special Triangles in a Unit Circle
Some angles are very commonly used and we can, therefore, just derive and memorize the exact trig ratios for those angles.
Within Q1 of a Unit Circle we can form 3 triangles: 60 – 30 – 90, 30 – 60 – 90 and 45 – 45 – 90 (the angle at the center of the circle is the RAA).
The ratios will be determined based on the diagram above, using SOH CAH TOA – the rule for determining the three primary trigonometric ratios within any right triangle.
There are also angles that are right on the axes, like 0, 90, 180, 270 and 360.
The above image provides trig ratios for those angles as well.
There is also a really cool way of determining the trig ratios of special angles using the fingers on your hand – check out how to do that.
When you travel around the Unit Circle, you can build right angle triangles that are based on the RAA (related acute angle) and the center of the circle. The new angle – PRINCIPAL ANGLE – will be the horizontal axis angle + or – the RAA with the sign of the ratio determined by the CAST rule.
For example, if we want to determine the exact value of sin150, here are the step that we should take:
- Determine the quadrant the angle is in: 150 is between 90 and 180, thus it is located in Q2.
- Determine the closest angle on the horizontal axis: that would be 180
- Add or subtract the given angle from the angle on the horizontal axis to determine the Related Acute Angle: in this case we subtract 180 – 150 = 30
- Determine the exact value of the trig ratio for the RAA (it will be the same value for the given angle): sin30 = 1/2
- Use CAST Rule to determine the sign of the ratio for the given angle: since 150 is in Q2 and we are looking for sin150, the ratio will be positive because in Q2 sine ratio is positive: sin150 = 1/2
In general, periodic behaviour is described as a relationship between an angle and a trig ratio of that angle within a circle. However, periodic behaviour can represent many relationships, such as time and height, etc. They all, however, are based on the concept of trigonometric ratios that repeat around the circle n-number of times.