Introduction to Functions
A function in mathematics is a relationship between two quantities, where for every input (independent variable) there is only one possible unique output (dependent variable).
Functions have been used in ancient India, Greece, Egypt, Persia, Central America, China, however, they were not called functions.
The very notion of a function as a relationship between an independent variable and a unique dependent variable was developed in the 17th century, when Rene Descartes used the term “function” to describe relationships between quantities in his book “Geometry”.
A function became officially called a function when Gottfried Wilhelm Leibniz formalized the term decades after Descartes used it in his book. And then Leonhard Euler created a notation to represent a function.
f(x) – is a function notation “function of x” – it does not mean multiplication or any other operation but rather expresses the dependent variable in terms of the independent variable.
The eight main types of functions are: linear, quadratic, cubic, absolute value, square root, rational, exponential and periodic.
Each one of those functions models a certain behaviour that we observe in real life and can be used to calculate a variety of things (speed, height of the object at a given time, the value of a vehicle and so on).
Functions are all around us and are extremely useful. Understanding how functions work and how they relate to everyday life situations helps us understand a number of phenomena and predict what might happen next if the pattern continues.
Learn more about different types of functions:
Domain and Range
Every function has an independent and a dependent quantity. The type of relationship between those two quantities defines the type of the function.
Sometimes, not all independent and not all dependent variable values would work for a particular type of relationship and they need to be defined according to that.
A set of input (independent variable) values for which the function is defined are called the DOMAIN of the function.
A set of output (dependent variable) values for which the function is defined are called the RANGE of the function.
NOTATION
- In order to demonstrate a contained set of values we use { }
- The E symbol means “is the element of”
- The capital R within the Domain or Range means “all real numbers”
- Vertical line | is there to separate restrictions
- The capital Z within the Domain or Range means “all integers”
Watch how to determine and state the domain and range for different functions using both a set and an interval notations:
Transformations of Functions
So you kick a ball. And then your sibling kicks the same ball. The ball won’t fly along the exact same identical trajectory. What if you are standing on a platform? The initial height of the ball changes and the maximum height will change, as well as the landing location.
All of the above is transformations of a basic quadratic function.
When we change the base graph of any function – we apply transformations.
Function transformations include:
f(x) = af((k(x – d)) + c
- reflection is the x-axis (a)
- reflection in the y-axis (k)
- vertical stretch or compression (a)
- horizontal stretch or compression (k)
- vertical shift up or down (c)
- horizontal shift left or right (d)
Depending on the type of the function, these transformations look slightly differently, but in general mean the same thing each time you apply them.
Watch how to transform different types of functions:
Inverse Functions
Just like every operation has its inverse operation (multiplication and division, addition and subtraction), every function has an inverse function.
Examples of inverse functions are: quadratic function and square root function; exponential function and logarithmic function.
Inverse function graphs are symmetrical about the line defined by the equation y = x.
In order to determine the equation of an inverse function to the given function we switch the independent and the dependent variables of the original function and express the dependent variable in terms of an independent one:
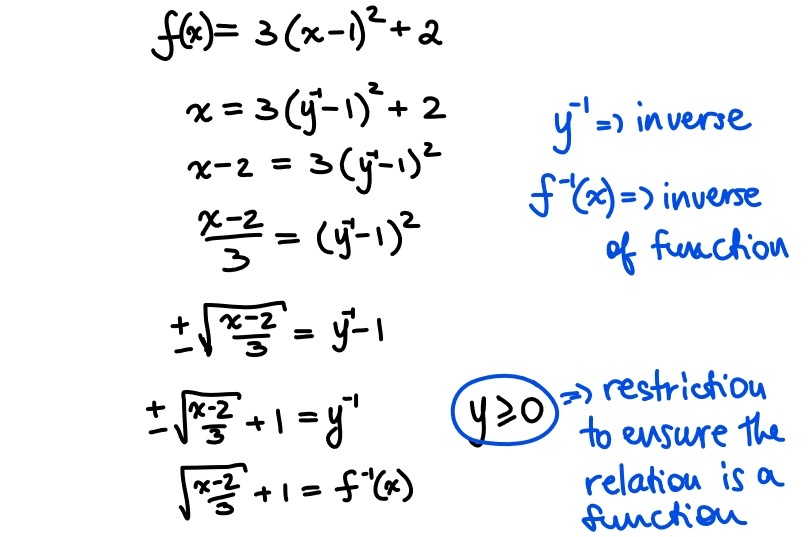
It is always important to ensure that the inverse relation is a function in order to be able to use a function notation.