Rational Exponents
Rational exponents (fractional exponents) are exponents that are fractions or rational expressions.
A rational exponent can be converted to its equivalent radical form.
Exponent laws can be applied to rational exponents in the same way they work for any other types of exponents.
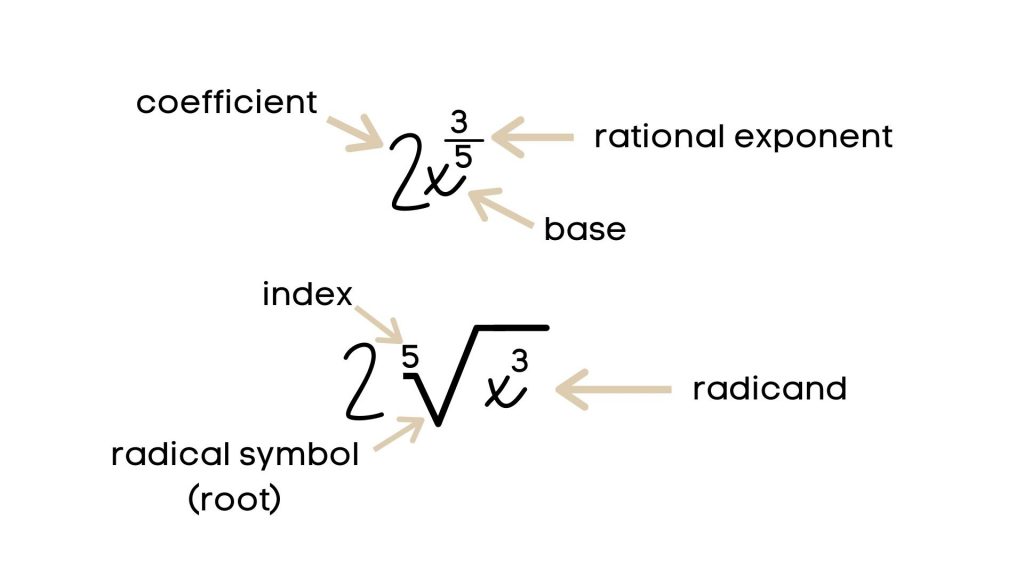
In general, in order to convert a rational exponent into a radical, keep the base as a radicand raised to the numerator exponent; place the denominator as an index of the radical symbol (root); place the coefficient in front of the radical symbol.
Multiplying and Dividing Expressions Containing Powers with Rational Exponents
In order to multiply expressions containing powers with rational exponents, we need to first multiply coefficients, then keep the corresponding base and add the corresponding exponents. Since the exponents are rational, a common denominator would need to found.
In order to divide expressions containing powers with rational exponents, we need to first divide or reduce coefficients, then keep the corresponding base and subtract the corresponding exponents. Since the exponents are rational, a common denominator would need to found.
Power of a Power Exponent Law with Rational Exponents
In order to raise an expression containing powers with rational exponents, we need to every part of that expression to the outside rational exponent. If there is a coefficient, it need to be raised to the outside rational exponent as per common rule raising any base to an exponent. For the powers containing rational exponents, the bases would have to remain the same, but the exponents would multiply by the outside rational exponent.
No matter what operation is performed on the expressions containing powers with rational exponents, it is important to follow exponent laws, pay attention to which part of the expression is raised to the exponent and which one is not (separate a coefficient), pay attention to signs (positive-negative).
Watch how to do operations on expressions containing powers with rational exponents: