Radical Expressions
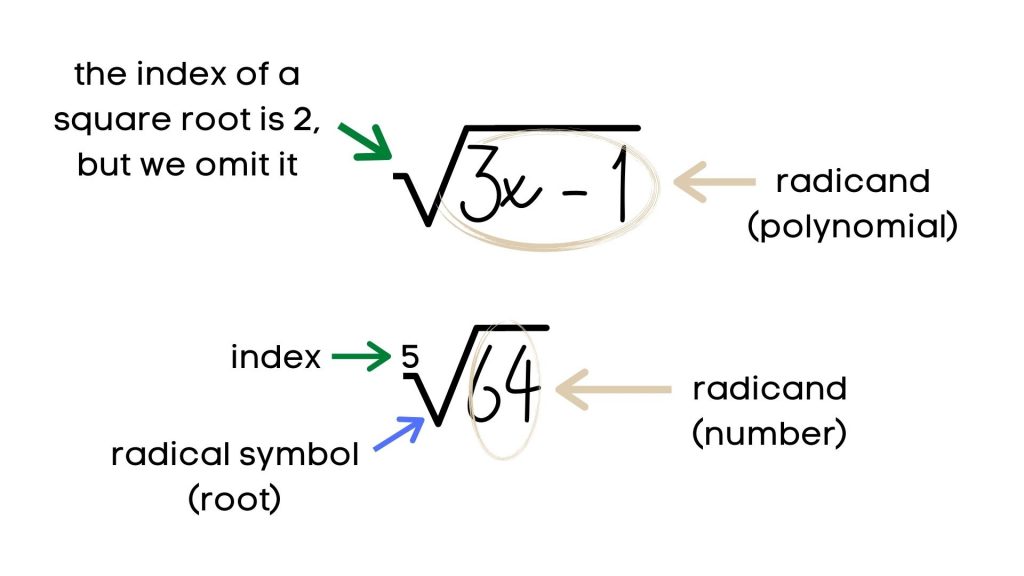
Radical expressions are expression containing a radical symbol (root) of a radicand (a number or a polynomial).
An index indicates the root value (3rd root, 5th root and so on).
Radical expressions are used to express values in their exact form instead of an approximate form.
Radicals are inverses of rational exponents.
Simplifying Radical Expressions
We can simplify radical expressions containing a square root by converting them into mixed radicals. In order to do that, a radicand needs to be split into a product of terms, at least one of which is a perfect square (for example, a 4 is a perfect square of 2). Then, take the square root of a perfect square and multiply it by the remaining radical as a coefficient.
We can add and subtract radicals that have the same root and radicand (just as we do with like terms in a polynomial).
We can multiply radicals by multiplying their coefficients and radicands separately.
Take a quizWatch how to simplify and perform operations on radicals:
Rationalize Denominator
Radicals can be a part of rational expressions. When there is a radical in the denominator, we need to rationalize the denominator that is eliminate the radical expression from the denominator. It is done so that it is easier to perform further computations involving that rational expression and so that the value of the expression is more obvious.
In order to eliminate a radical (most commonly a square root) containing a radicand that is a number from the denominator, just multiply both the numerator and the denominator of a rational expression by the radical.
In order to eliminate a radical containing a sum or a difference of two terms, one of which is a square root radical, multiply both the numerator and the denominator of a rational expression by a conjugate of the expression in the denominator. A conjugate pair is, for example, (x – 1) and (x + 1) – two expressions that differ only by their sign. The product of such conjugates will always result in a difference of squares – in the case of multiplying the expressions with a square root term, such product will help eliminate the root.
Watch how to rationalize a denominator: