Rational Expressions

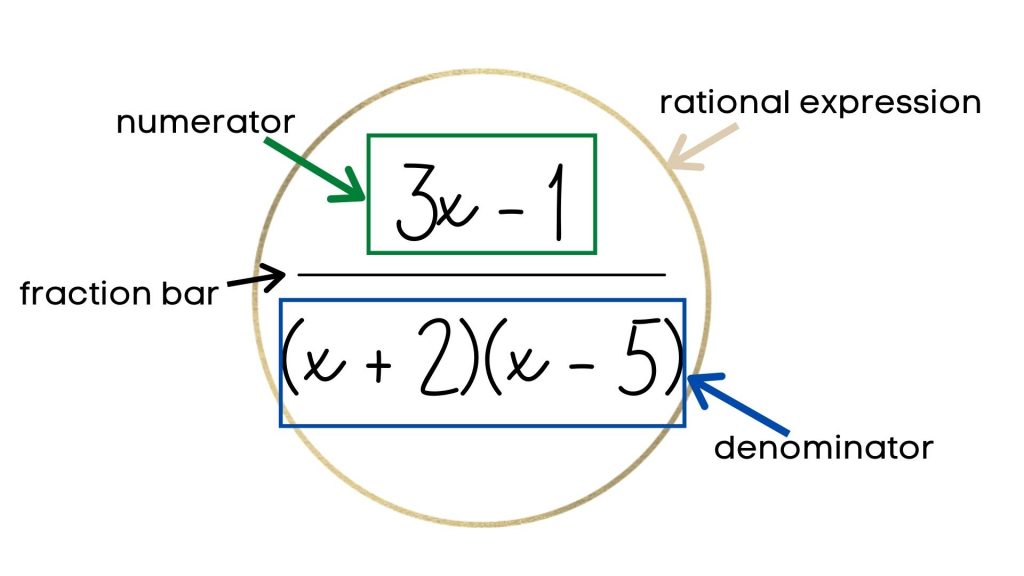
A rational expression is a quotient of two polynomial expressions.

It looks like a fraction, where both the numerator and the denominator are polynomials (a polynomial in the numerator can be a constant, but a polynomial in the denominator should be of degree 1 or higher).

Since a rational expression contains one or more variables in the denominator, restrictions need to be set such that denominator does not end up being equal to zero. This is necessary, because we cannot divide by a 0, the result is undefined.

Learn how to identify and set restrictions on the denominator of a rational expression:

Rational expressions can contain factored and non-factored polynomials (polynomials in standard or expanded form). In order to state restrictions and simplify such rational expressions, we need to factor their numerator and denominator first.

Take a quiz

Simplifying Rational Expressions

Sometimes a rational expression is not given in its simplest form and needs to be simplified further.

The restrictions in this case must be stated on the original expression. Once the restrictions have been set, the expression can be simlified.

To simplify a rational expression means reducing coefficients and powers with corresponding bases, as well as reducing identical factors in the numerator and the denominator.

Take a quiz

Here is how to simplify rational expressions:

Adding and Subtracting Rational Expressions

Rational expressions can be added and subtracted. The processes are very similar to those of adding and subtracting fractions.

• First, the numerators and the denominators of the rational expressions need to be fully factored.
• Second, state the restrictions on each original denominator.
• Next, create a common factor by multiplying all existing unique factors from the denominators of each rational expression that is being added or subtracted.
• After that, adjust the numerator of each rational expression by the missing factor in the original denominator.
• Then, expand and simplify the numerator. Factor the resulting numerator and see if any of the factors in the common denominator and the new combined denominator can be reduced.

Take a quiz

Watch how to add and subtract rational expressions:

Multiplying and Dividing Rational Expressions

The processes of multiplying and dividing rational expressions is very similar to those of multiplying and dividing fractions. However, different from from the processes of adding and subtracting rational expressions.

When multiplying rational expressions, factor the numerator and the denominator of each expression first, state the restrictions on the original denominators and then see if any coefficients and factors in could be reduced. After that, multiply the numerators and the denominators across.

When dividing rational expressions, factor the numerator and the denominator of each expression first, then state the restrictions on the original denominators. After that, take the reciprocal of the second rational expression (of the dividend), change operation from division to multiplication and state the additional restrictions on the new denominator (former numerator). Then, reduce the coefficients and factors if possible and multiply numerators and denominators.

Here is a video on how to multiply and divide rational expressions:

Take a quiz