Search block

Cosine Law. Sine Law. Ambiguous Case of Sine Law

When we need to determine angle measure or side lengths within the non-right triangles, we use Cosine Law and Sine Law.

Cosine Law is used in two cases: SAS and SSS

  1. When we are given all three sides, no angles and are looking for an angle
  2. When we are given 2 sides and a contained angle are looking for the side length that corresponds to the given angle.
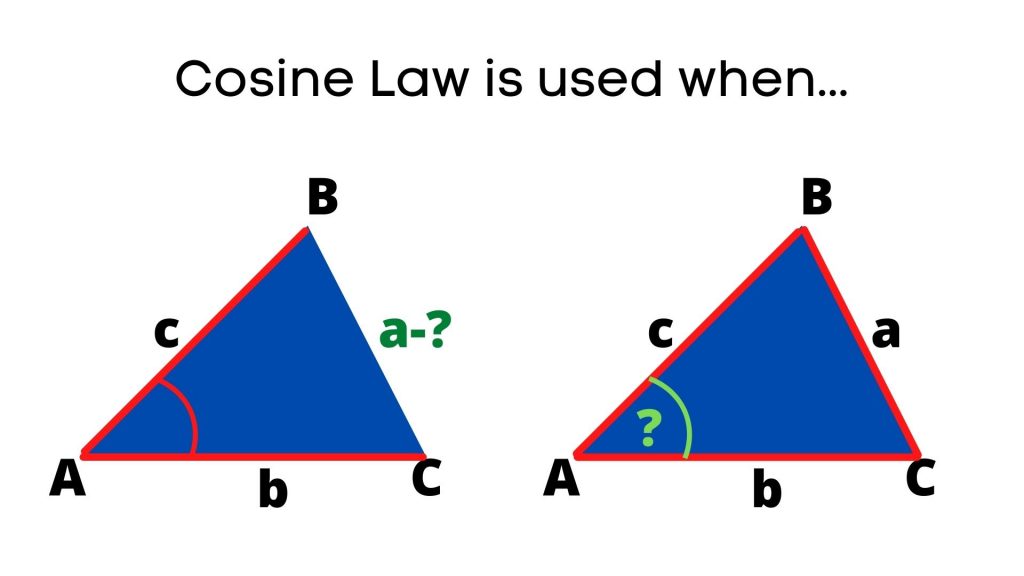
when to use cosine law

Cosine Law Formula(e)

c^2=a^2+b^2-2abcosC

a^2=b^2+c^2-2bccosA

b^2=a^2+c^2-2accosB

When solving for an angle, the formula needs to be rearranged and the last step is always taking the inverse ratio to get the measure of the angle.

Sine Law is used in cases when Cosine Law cannot be used.

Usually when we have pairs of corresponding sides and angles, within one of which either a side or an angle is unknown: SAA or SSA

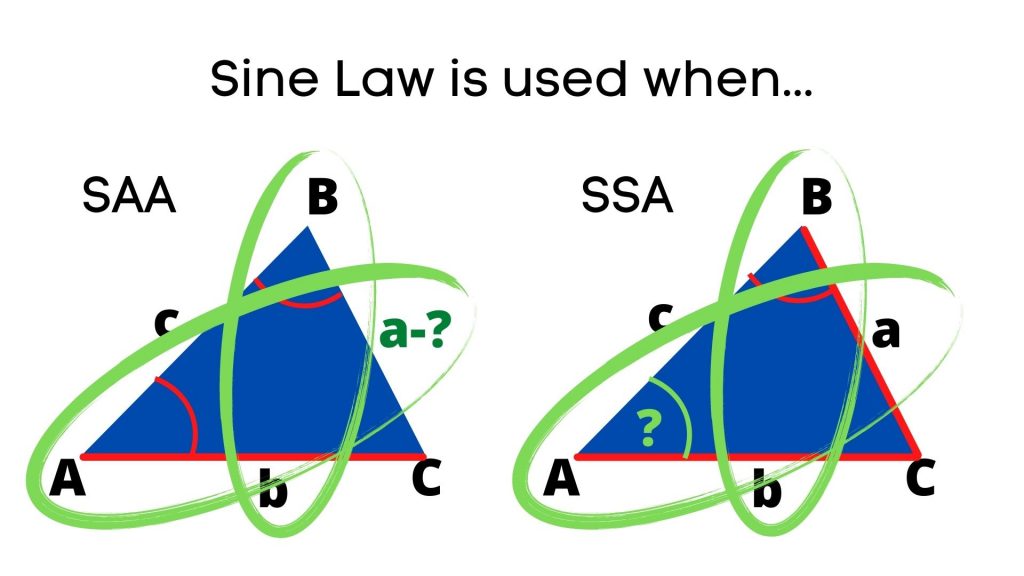
when to use sine law

Sine Law Formula

\frac{sinA}{a}=\frac{sinB}{b}=\frac{sinC}{c}

Normally, we set up an equation involving two ratios provided and cross-multiply to isolate for the unknown value.

Take a quiz

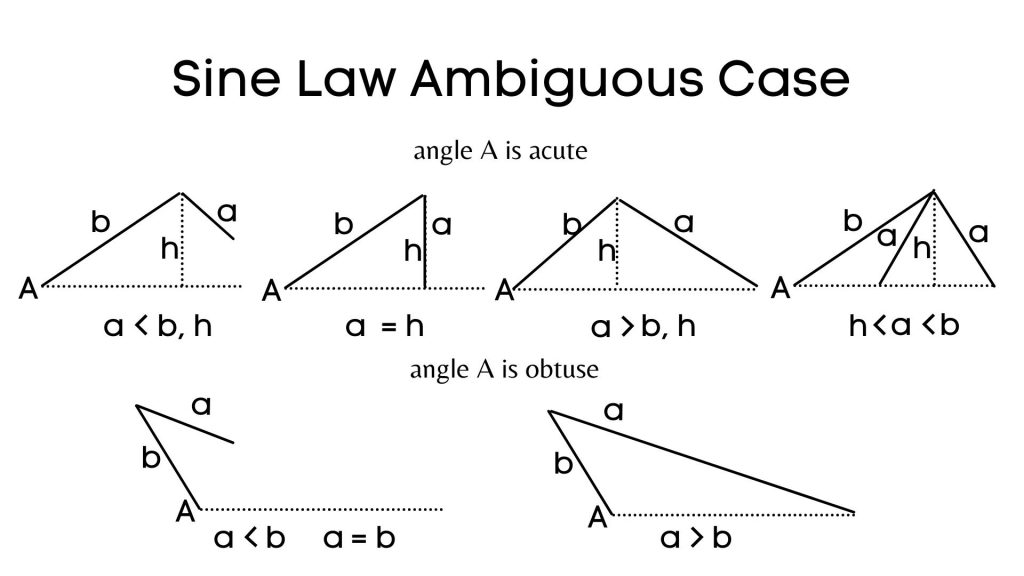
Ambiguous Case of Sine Law

Whenever we are given two sides and an angle and are lookin for another angle, we can use Sine Law. However, we need to be aware of the possibilities that the relationships between the given measurements could results in. Sometimes, the relationship between the sides and an angle do not even produce a triangle. In other cases they may result in two possible triangles and we need to consider both situations. This is called an Ambiguous Case of Sine Law.

Below is a diagram of possible outcomes depending on the measurements given:

Sine Law Ambiguous Case outcomes

Learn more about Cosine Law, Sine Law and the Ambiguous Case of Sine Law and see worked examples by watching the video lesson: