Solving Trigonometric Equations (Degrees)
Trigonometric equations are equations that allow us to determine the relationship between the input and the output of trigonometric functions, as well as solve for a specific value or values of input that produce the desired output.
Trig equations can be linear and quadratic. We may sometimes also need to use trigonometric identities to solve trig equations.
When we change the period of a function, it affects how many solutions the equation has on a particular interval and what types of solutions.
Unless the periodic function represents a particular situation relating quantities other than angles and trigonometric ratios, we are solving trigonometric equations to determine the measures of all possible angles that produce a certain trigonometric ratio.
Some trigonometric equations could be solved by considering special triangles, as the trigonometric ratios within those equations are given as exact trigonometric ratios of the 30, 60, or 45 degree angles, as well as of the angles that fall on the axes.
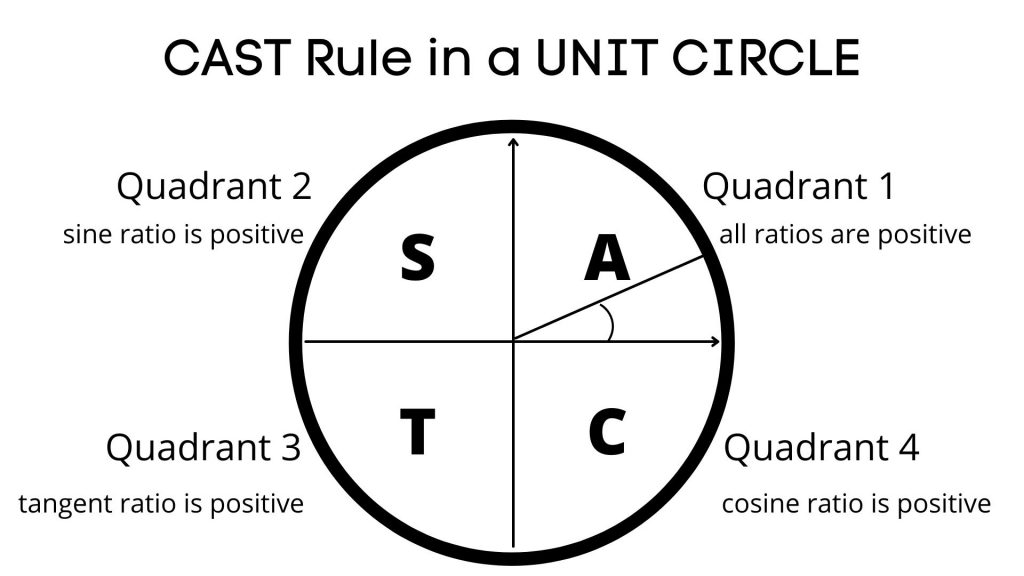
It is also useful to understand and operate the Unit Circle well when solving trigonometric equations, as well as know the principle behind the CAST rule that determines the sign of a particular trig ratio inside the unit circle. The diagram below explain this process.
Strategies for Solving Trigonometric Equations
- Decide whether the given trigonometric equation is linear or quadratic
- Check to see if the equation is expressed as a single trigonometric ratio, otherwise use trig identities to express it in terms of a single trigonometric ratio
- If the equation is a linear trig equation, determine if the ratio is given in the exact form and corresponds to the trigonometric ratios of one of special angles or angles on the axes. If it does, use a special triangle and a CAST rule to determine solutions.
- If the equation is a linear trig equation and a trigonometric ratio is not that of one of the special angles, use your calculator to determine the inverse of the ratio. Determine the inverse of the positive ratio to get the Related Acute Angle if the given ratio is negative, then use the CAST rule to find solutions.
- If the equation is a quadratic trigonometric equation, factor it first. Then set each linear factor to 0 and isolate for the appropriate trigonometric ratio. Next, solve each one of the resulting linear equations as per steps 3 or 4 above.
- Always check the interval over which you are being asked to state the solutions.
- If there is a change in the period, first determine the solutions disregarding the change in the period and then divide the resulting values by the k-value of the equation. It is crucial to check how many solutions would fit within the interval when there is a change in period. For every solution within additional rotations add the period to the original solutions.
- Go back and review your steps and solutions. It is common to make small mistakes when solving trigonometric equations.
Watch how to solve linear and quadratic trigonometric equations, as well as equations that contain different trig rations and where trigonometric identities must be used.