Solving Trigonometric Equations (Degrees)
Trigonometric equations are mathematical equalities that help us understand how angles relate to the outputs of trigonometric functions, like sine, cosine, and tangent. Basically, they allow us to figure out what angle (or angles) will give us a specific trigonometric ratio.
These equations can be either linear or quadratic, and sometimes we need to use trigonometric identities—essentially rules that connect different trigonometric functions—to solve them more easily.
One key thing to remember is that the period of a function is important. It tells us how often the function repeats its values, and changing the period can alter how many solutions we find within a certain range, as well as what those solutions look like.
Unless we’re dealing with a specific scenario involving a periodic behaviour where something other than angles and trigonometric ratios is considered, the main goal in solving trigonometric equations is to figure out all the possible angles that will give us a certain trigonometric ratio. This is really useful in areas like physics and engineering, where trigonometry helps us model all sorts of wave-like phenomena.
Some trigonometric equations could be solved by considering special triangles, as the trigonometric ratios within those equations are given as exact trigonometric ratios of the 30, 60, or 45 degree angles and of the angles that fall on the axes.
Understanding and effectively using the Unit Circle is essential when solving trigonometric equations. It’s also important to grasp the principle behind the CAST rule, which helps determine the sign of a specific trigonometric ratio within the Unit Circle. The diagram below illustrates this process.
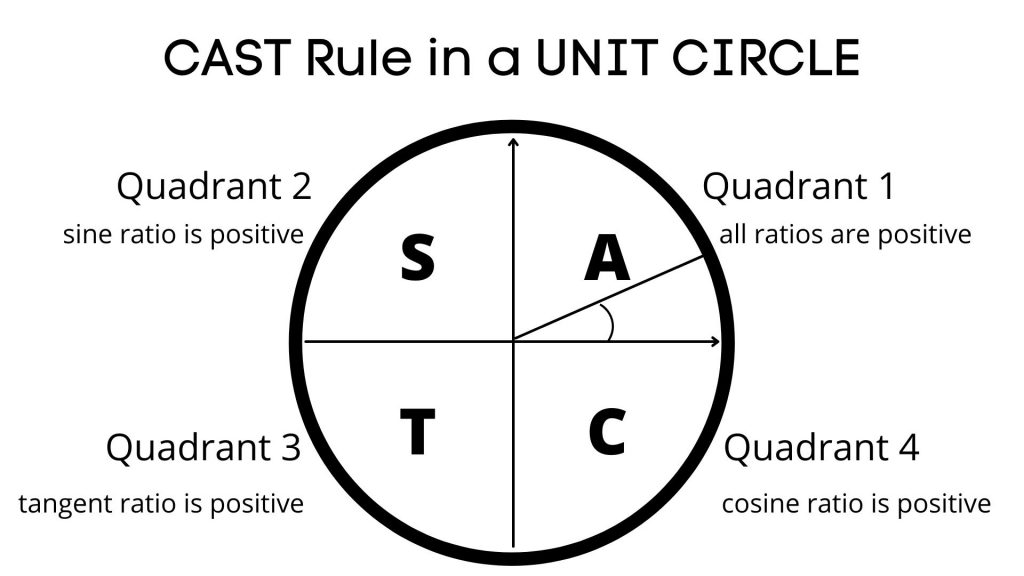
Strategies for Solving Trigonometric Equations
- First, assess whether the trigonometric equation at hand is linear or quadratic. This initial determination sets the stage for your solution strategy.
- Next, strive to express the equation as a single trigonometric ratio. If it isn’t already in that form, employ trigonometric identities to simplify it accordingly.
- For linear trigonometric equations, evaluate whether the ratio is in exact form and corresponds to the trigonometric ratios associated with special angles or angles on the axes. If it does, leverage a special triangle and the CAST rule to confidently identify your solutions.
- If the equation is linear but the ratio does not correspond to one of the special angles, use your calculator to find the inverse of the ratio. If the given ratio is negative, first find the inverse of the positive ratio to obtain the Related Acute Angle, and then apply the CAST rule to discover all possible solutions.
- When tackling quadratic trigonometric equations, begin with factoring. Set each linear factor equal to zero to isolate the necessary trigonometric ratio. Then proceed to solve each resulting linear equation using steps 3 or 4.
- It’s essential to always verify the specific interval for which you need to present your solutions. Clarity here ensures you provide accurate answers.
- In cases where there’s a change in the period, first identify the solutions without factoring in the period change. Then, divide the resulting values by the k-value of the equation. This method will help you determine how many solutions fit within the given interval. Remember, for each solution within additional rotations, simply add the period to the original solutions.
- Finally, meticulously review your steps and solutions. Trigonometric equations can harbour small mistakes, so careful verification can safeguard against errors and lead to clearer, more precise results. Trust in your process and take pride in your findings!
Watch how to solve linear and quadratic trigonometric equations and equations containing different trig ratios, and where trigonometric identities must be used.