The Quadratic Formula. Its Origin and Application

The quadratic formula is one of students’ most favourite mathematical formulas. It can be quite easily memorized. Students eagerly use it to solve quadratic equations of the form ax² + bx + c = 0. However, not everyone knows why we use it and where the quadratic formula comes from.

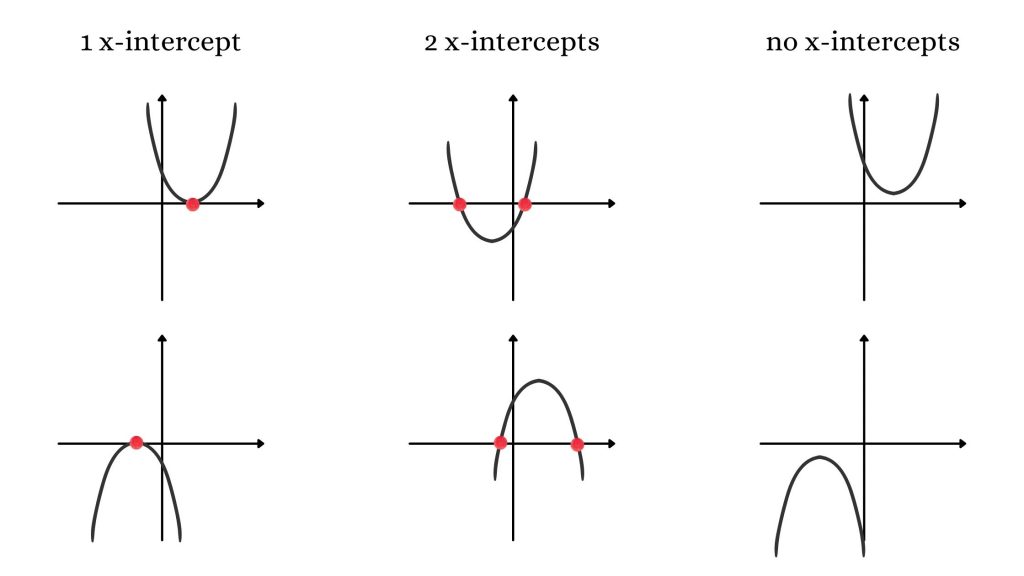
When we are trying to determine the x-intercepts of a parabola (a graph of a quadratic function) represented by a certain quadratic equation, we are solving that equation. Quadratic equations may have 1 solutions, 2 solutions or no solutions. This means that the corresponding parabola has 1, 2 or no x-intercepts. Sometimes, the x-intercepts are not “nice” numbers (irrational) and it is difficult to use factoring methods to solve an equation to determine the x-intercepts. This is when the quadratic formula could be used.

Let’s consider, for example, quadratic function given by the equation f(x) = 6x² + x – 2.

When we want to determine the x-intercepts (roots, zeros) of the graph of the above function, we need to make the equation equal to 0 and solve for x(s): 6x² + x – 2 = 0.

This equation is factorable and can be solved using one of the factoring techniques, such as decomposition. The process results in the factored form (2x – 1)(3x + 2) = 0.

Therefore, the parabola crossed the x-axis at two points: (1/2, 0) and (-2/3, 0).

This was not to difficult to figure out.

Now, if the function is given by the equation f(x) = 4x² – 6x + 1, try graphing it using a graphing calculator. It has two x-intercepts, but it is very difficult to determine their exact values by looking at the graph or by using any of the factoring techniques. In such case, the quadratic formula needs to be used.

What is the Quadratic Formula and How to Use It

The quadratic formula can be used when the equation of a quadratic function is given in the standard form:

f(x) = ax² + bx + c, where a and b are coefficients, c is a constant value (also y-intercept (0, c)).

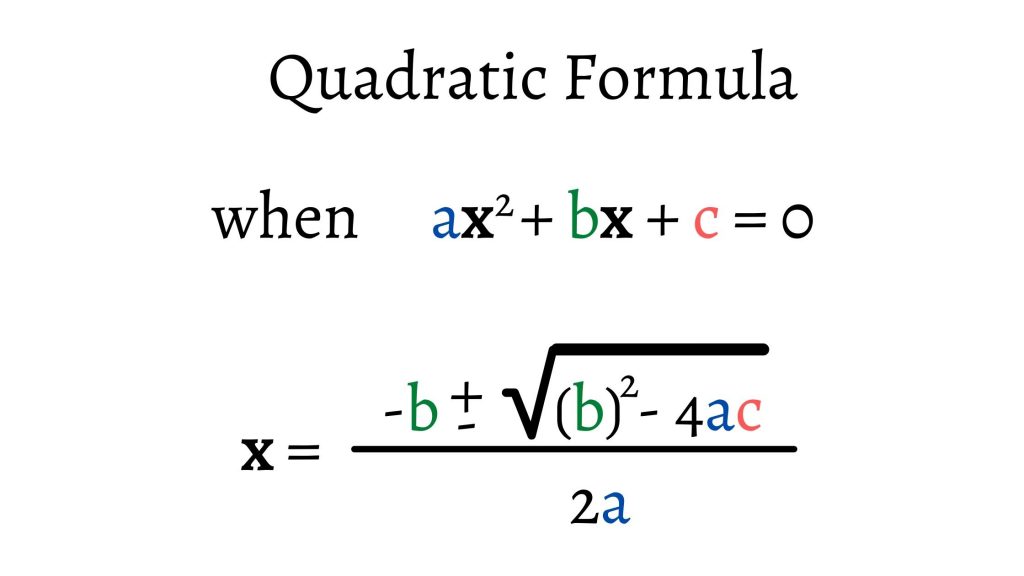
Things to keep in mind when using the quadratic formula:

The equation must be in standard form and must equal to 0 on one side
The values of a, b and c do not include the variable x from the equation
The signs in front of a, b and c in the equation are “attached” to them
When b is negative and squared under the square root – it must be in brackets
First complete all operations in the numerator and only then divide by the denominator
Depending on the problem, you may need to state the solution(s) in the approximate form or the exact form. The solution(x) in the exact form contain radicals (unless a solution is an integer or a rational number).

The Discriminant

The quadratic formula is a rather useful and straightforward tool for solving quadratic equations. However, it is sometimes frustrating when you set up the formula and evaluate half of it only to find out that it cannot be evaluated further. The equation of the function has no solutions – the parabola has no x-intercepts (see the diagram above).

This is when the Discriminant – the expression under the square root of the quadratic formula – comes to the rescue, offering more efficiency and clarity in terms of how many, if any, solutions to expect.

Let’s consider the equation of the function we already discussed above and determine how many x-intercepts and what types of x-intercepts it has:

$F(x)=4x^{2}-6x+1$

$4x^{2}-6x+1=0, a=4, b=-6, c=1$

$D=(b)^{2}-4ac$

$D=(-6)^{2}-4(4)(1)$

$D=36-16$

$D=20, D> 0$ therefore, there are 2 distinct real solutions (x-intercepts)

Now let’s use the complete quadratic formula to determine the exact and approximate values of those two solutions:

$x=\frac{-b\pm \sqrt{(b)^{2}-4ac)}}{2a}$

$x=\frac{-(-6)\pm \sqrt{20}}{2(4)}$

$x=\frac{6\pm \sqrt{4\times 5}}{8}$

$x=\frac{6\pm 2\sqrt{5}}{8}$

$x=\frac{3+\sqrt{5}}{4}, x=\frac{3-\sqrt{5}}{4}$

$x\approx 1.309, x\approx 0.191$

Why Do We Say “Real” Solutions?

There are several number systems that we consider in mathematics.

Natural Numbers, Integers, Rational Numbers, Irrational Numbers, Real Numbers, Complex Numbers and beyond.

The Real Number System includes Natural Numbers, Integers, Rational Numbers and Irrational Numbers. Real numbers are numbers that we can evaluate and determine knowing methods known to us and they produce quantities that correspond to what we experience in real life.

The Complex Number System includes all previous number systems and imaginary numbers, where we consider values that do not define quantities that we operate every day. A Complex Number System is based on a value of i that is equal to a square root of a negative number 1 (whereas we know that in the real Number System it is impossible to square root a negative since no base, positive or negative, when squared, will result in a negative value).

Imaginary Unit $i=\sqrt{-1}$

Therefore, in the Complex Number System we can actually evaluate square roots of negative numbers:

$\sqrt{-4}=\sqrt{4}\times \sqrt{-1}=2i$

It is important to remember that the Complex Number System exists and to understand how it works, because sometimes the expression for the Discriminant may be negative – so we end up taking a square root of a negative number.

And while the equation of the function is such case will have no real solutions, it may still have those special, complex solutions based on i.

The Origin and the Proof of the Quadratic Formula

Historians have established that “square” mathematics dates back to as far as 1700 BCE, when the Babylonians working with areas and perimeters of rectangles, trying to determine dimensions.

Then the Ancient Greeks were trying to tackle the same types of problems.

However, both the Babylonians and the Greeks working their solutions out geometrically as the concepts of Algebra and the algebraic notation were not yet developed.

Then, in 825, a famous Persian mathematician Muhammad bin Musa al-Khwarizmi used symbols and the concept of an equation. He created a method to solve a quadratic equation, but assumed that coefficients a, b and a constant c in the standard form equation could only be positive values. Thus, his equations were always equal c on one side, rather than 0.

In 1545, a European mathematician Girolamo Cardano, considered the geometric and al-Khwarizmi’s methods together and figured out how to solve quadratic equations that would allow for all real solutions and even imaginary numbers (this helped further develop the Complex Number System).
In 1637, René Descartes published La Géometrie that included the Quadratic Formula in the exact form we use it today.

An Algebraic Proof of the Quadratic Formula

$ax^{2}+bx+c=0$ $\times \frac{1}{a}$ (a-s will be reduced to 1 as a result)

$x^{2}+\frac{b}{a}x+\frac{c}{a}=0$

$x^{2}+\frac{b}{a}x=-\frac{c}{a}$

$x^{2}+\frac{b}{a}x+(\frac{b}{2a})^{2}=-\frac{c}{a}+(\frac{b}{2a})^{2}$ (completing the square)

$(x+\frac{b}{2a})^{2}=-\frac{c}{a}+\frac{b^{2}}{4a^{2}}$

$(x+\frac{b}{2a})^{2}=-\frac{4ac}{4a^{2}}+\frac{b^{2}}{4a^{2}}$

$(x+\frac{b}{2a})^{2}=\frac{b^{2}-4ac}{4a^{2}}$

$x+\frac{b}{2a}=\pm \sqrt{\frac{b^{2}-4ac}{4a^{2}}}$

$x=-\frac{b}{2a}\pm \frac{\sqrt{b^{2}-4ac}}{2a}$

$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$

When the expression under the square root (the Discriminant) results in a negative value, there are no real solutions, but we can still determine complex solutions as discussed above.

Real Life Application of The Quadratic Formula

A ball is thrown upwards from a platform above the ground and the ball’s path can be modelled by the following equation

$h(t)=-16t^{2}+5t+15$

Where h(t) is the height in meters and t is the time in seconds.

When will the ball hit the ground?

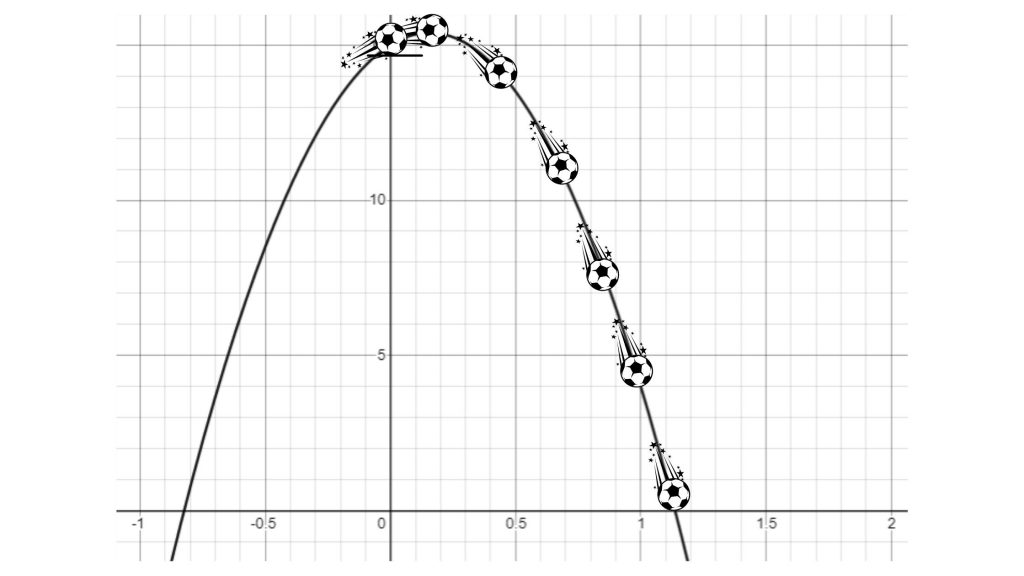
In order to answer the question, we need to understand that at the ground the height of the ball is 0 m.

Therefore, h(t) = 0, then solve for t in seconds.

$-16t^{2}+5t+15=0$

$t=\frac{-5\pm \sqrt{25-4(-16(15)}}{2(-16)}$

$t_{1}=\frac{-5+\sqrt{985}}{-32}, t_{2}=\frac{-5-\sqrt{985}}{-32}$

$t_{1}\approx -0.8, t_{2}\approx 1.1$

Since we are considering time in seconds, the -0.8 solution is outside of our domain. Therefore, the ball will hit the ground after approximately 1.1 seconds.

The Quadratic Formula. Its Origin and Application

What is the Quadratic Formula and How to Use It

The Discriminant

Why Do We Say “Real” Solutions?

The Origin and the Proof of the Quadratic Formula

An Algebraic Proof of the Quadratic Formula

Real Life Application of The Quadratic Formula

One thought on “The Quadratic Formula. Its Origin and Application”

Real World Applications of Linear Systems

Trigonometry On Fingers

How to Identify and Analyze Jump Discontinuity in Functions

The Crucial Role of Mathematics in Construction: A Comprehensive Exploration