Lesson 1: Natural Numbers up to 1000
Numbers are integral to our daily lives, serving essential purposes in counting, measuring, ordering, and estimating.
Natural numbers — such as 0, 3, 6, 10, 204, and 1000 — are the positive numbers we rely on most frequently to quantify and organize the world around us.
Embracing the power of these numbers enhances our ability to understand and navigate various aspects of life.
In mathematical terminology, numbers used for counting are called “cardinal numbers” and numbers used for ordering are called “ordinal numbers“.
TWO and SECOND, FIVE and FIFTH, THIRTY and THIRTIES …
Mathematicians use N to represent a set of all natural numbers. The set of natural numbers is an infinite set. This infinity is called countable infinity.
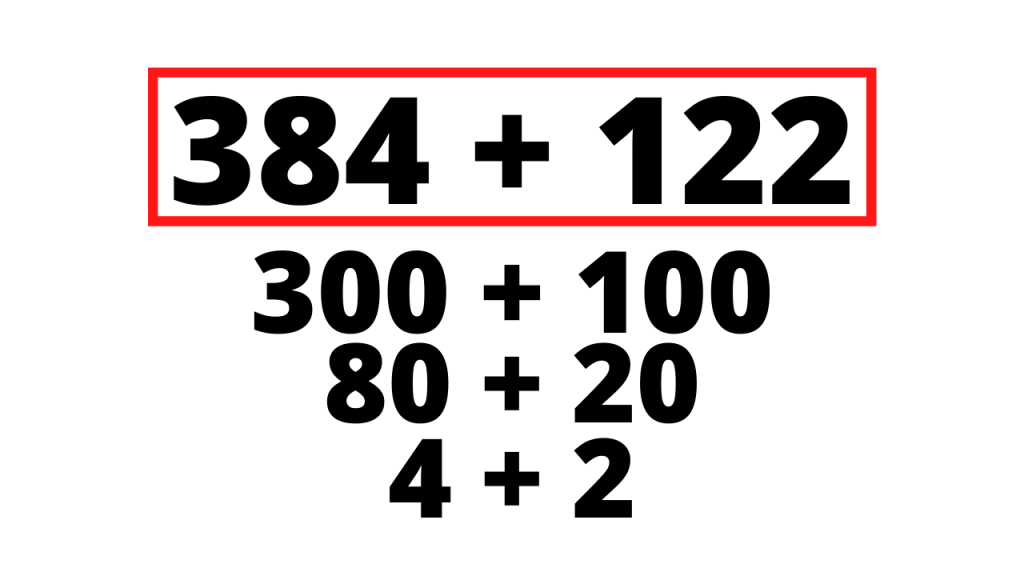
Properties of Natural Numbers
- 0 is a natural number (but some mathematicians do not include it in the list of natural numbers)
- Every natural number has a number that comes after it and is also a natural number
- 0 does not come after any natural number
- If the number that comes after x is equal to the number that comes after y, then x = y
Operations with Natural Numbers up to 1000
We can perform a range of operations with natural numbers, including ordering, comparing, adding, subtracting, multiplying, and dividing. Understanding how to manipulate these numbers is fundamental in mathematics.
In this lesson, we will focus on adding and subtracting natural numbers up to 1000.
A key strategy for doing this effectively involves breaking numbers down based on their place value. Place value refers to the value of each digit in a number, depending on its position. This concept is critical for accurate calculations.
For instance, the number 345 can be decomposed into its individual place values: 300 (which represents three hundreds), 40 (which represents four tens), and 5 (which represents five units). When adding this number to another number of a similar structure, it is often beneficial to add these components separately.
By doing so, we simplify the process and reduce the chances of error, making our calculations clearer and more manageable.
This method not only enhances accuracy but also strengthens our overall understanding of numbers and their relationships in arithmetic operations.
Subtracting two natural numbers does not always result in a natural number. For example, 213 – 321 will produce a negative number, that is no longer a member of a set of natural numbers, but rather a negative integer.
Place value of digits within a number is important when doing operations with natural numbers, as corresponding digits need to be added/subtracted respectively.
