Lesson 7: Simplifying Expressions with Exponents
Simplifying expressions with exponents is an important skill that is required to comfortably work with different types of functions and their equations. It is especially useful when solving polynomial and rational equations.
We already looked at the concept of exponent in previous grades. However, we only operated integer exponents.
In this lesson we are moving further and learning about rational exponents and their properties.
A rational exponent is an exponent expressed as a fraction m/n.
A power containing a rational exponent can be transformed into a radical form of an expression, involving the n-th root of a number.
The n-th root of a number a is another number, that when raised to the exponent n produces a.
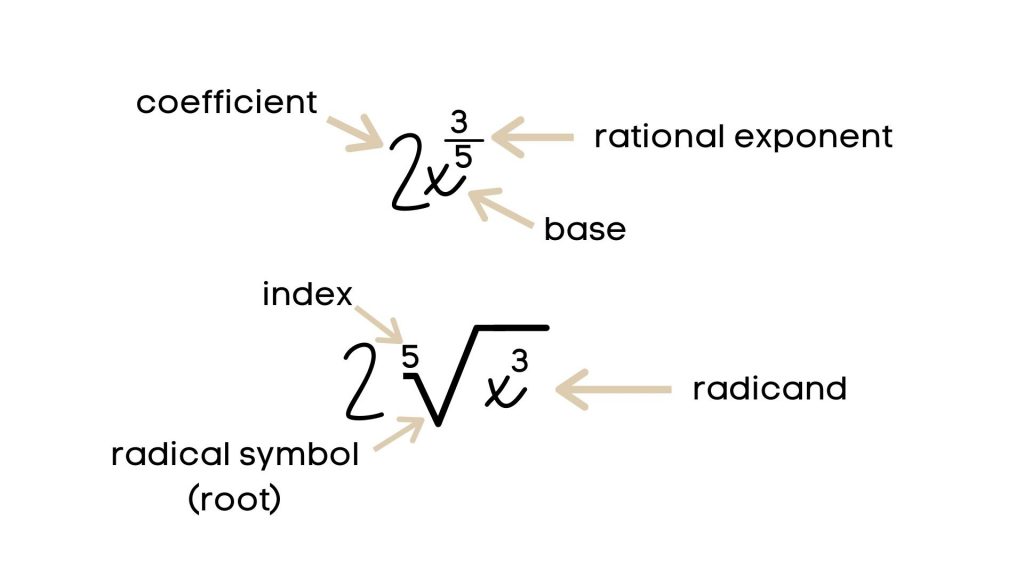
We are also practicing how to use negative exponents in this lesson and discussing the difference between even and odd exponents.
In addition, we are analyzing the base of 0 raised to a rational exponent.
Simplifying expressions with exponents requires us to use a variety of exponent laws and properties. We may start with a really complex expression that, when simplified, could result in one variable or a number.
For example, in order to simplify the following expression, it makes sense to express what we can in terms of the same base and use exponent laws:
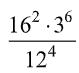
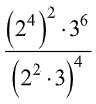
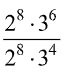
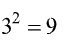
As you can see, we used the Power law of exponents, as well as the quotient law to simplify this expression. It is not uncommon that these simplifying expressions with exponents requires us to think a little bit outside of the box, see ways that we can express and transform numbers in order to apply laws to them.
Exponents Short Animation
Simplifying Expressions with Exponents Quiz
