The Wheat and a Chessboard. Exponents.

The Wheat and a Chessboard is an ancient legend about the inventor of chess, who showed his invention to the Emperor of India for the first time. The Emperor was very impressed by the invention.

He liked it so much, that he offered any reward the inventor could wish for.

The inventor said: “My wish is very simple.

There are 64 squares on the chessboard and

for the first square I wish only 1 grain of wheat,

for the second one I wish 2 grains,

for the third one I wish 4 grains,

for the fourth I wish 8 grains,

for the fifth I wish 16 grains

and so on for all the 64 squares”.

The emperor was not good at math and was surprised that the inventor seemed to have asked for such a small reward.

So the Emperor ordered his treasurer to give the inventor the wheat grains for all the squares as requested.

A few days later the Emperor asked his treasurer whether the chess inventor has been rewarded.

The treasurer informed the emperor that the reward turned out to be an astronomical sum, greater than all the wheat that could be gathered in many centuries.

This legend illustrates how powerful the exponents can be.

Let’s go through the legend once again, but this time, we will look at how the numbers were calculated to determine the amount of wheat grains.

The following chessboard contains 64 squares and illustrates how many grains of wheat each square the inventor asked for represents.

If we look at the numbers on the squares, we can see that each subsequent square contains the number that is two times greater than the previous one.

We can use exponents to demonstrate this relationship.

An exponent of a number tells us how many times the number has been multiplied by itself.

Expressions that represent repeated multiplication of the same number are also called Powers

On the chessboard:

1st square: 1

2nd square: 2¹

3rd square: 2²

4th square: 2³

5th square: 2⁴

6th square: 2⁵

n-th square: 2^n-1

So each subsequent number is 2 times greater than the previous one.

The number in the first square can be represented as 2⁰ (any number except 0 to the power of 0 is 1).

In order to calculate the total amount of wheat in all of the 64 squares, we need to add up all of the powers, from 2⁰ to 2⁶³.

Now if we look closer at the sequence, we can definitely conclude that the elements of the sequence represent geometric progression, stating that any element in the geometric progression can be evaluated as:

a_n = a₁r^n-1

where r is a common ration, a_n is the n-th term and a₁ is the first term in the sequence.

The sum of all numbers in geometric progression is called Geometric Series.

We will look at the detailed explanation of geometric progression and series in the upcoming blog posts, but for now here is the formula for the geometric series:

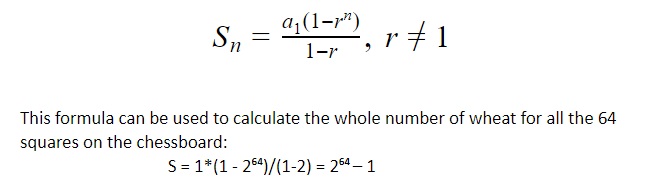
So, according to the above solution, which also involves operations in brackets, on the entire chessboard the number of wheat grains is equal to 18,446,744,073,709,551,615 weighing about 1,199,000,000,000 metric tons.

This is about 1645 times the global production of wheat in 2014!

Want to review exponents? Try this quick online quiz.