Completing a Square Geometrically

In high school, we study questions known as quadratic equations. However, we do not really talk about how they were invented and why. Well, quadratic equations are called quadratic because originally ancient mathematicians were using geometrical shapes – rectangles and squares – to figure out the area, the perimeter, the position of something, the maximum and minimum values in a strictly geometric way. The Babylonians, the Egyptians and the Greeks were all solving quadratic types of problems using geometry. In Latin, square is “quadratum”, thus, quadratic equations are based on a concept of a square.

Quadratic equations in their algebraic form, as we know them today, were first discovered by a Persian scholar, Al-Khwarizmi. While he was not calling them ‘quadratic equations’, they were based on the dimensions of a square and eventually borrowed the Latin name of the shape “quadratum”.

Al-Khwarizmi was able to solve quadratic equations using a method we now know as completing a square.

The Problem of Two Rooms

In the ancient times, people who were involved in construction and dividing land required some mathematical tools to solve challenging problems they were encountering.

One of the problems which Al-Khwarizmi managed to solve by combining Geometry and Algebra was related to building an accommodation consisting of two rooms.

Say, you were given a piece of land with an area equal to 39 m² and you need to build a 2-room accommodation on it, where the 1st room is a square and one of the sides of the 2nd room is equal to the side of the 1st room, but the 2nd side of the 2nd room is 10 meters. What is the side length of the 1st room?

So, the total area is equal to 39 m² and we need to find the value of x.

Let’s express the total area as the sum of the area of the square and the area of the rectangle:

x² + 10x = 39

At the time of Al-Khwarizmi there were no mathematical formulas to solve this kind of problem, so he decided to try to divide the 2nd room into two parts and arrange them differently as shown below:

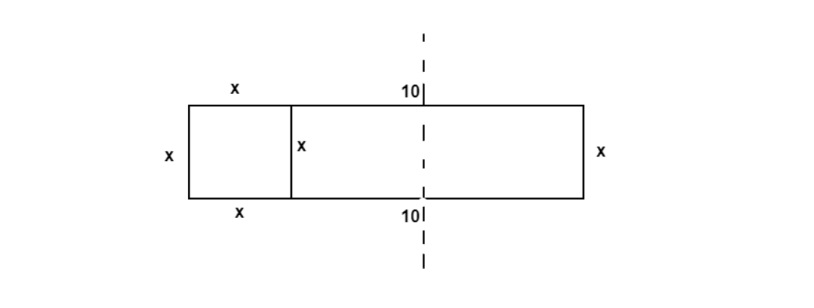
rectangle split into other two rectangles

This resulted in the following combination of three figures:

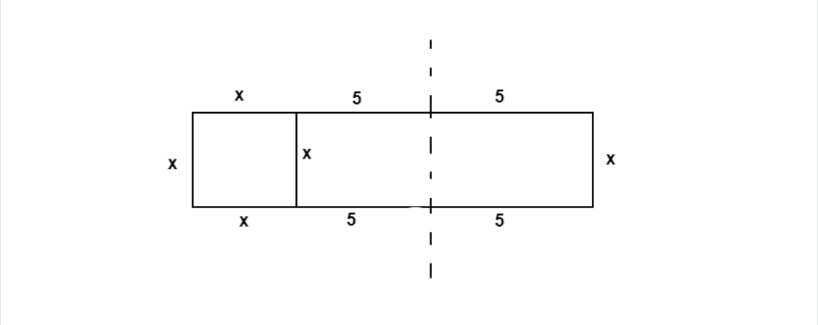
Then, the rectangles were shifted and combined together in the following formation:

When Al-Khwarizmi looked closely at the rearranged formation, he thought:

“What if I add one more shape at the right-bottom position, which will definitely be another square?”

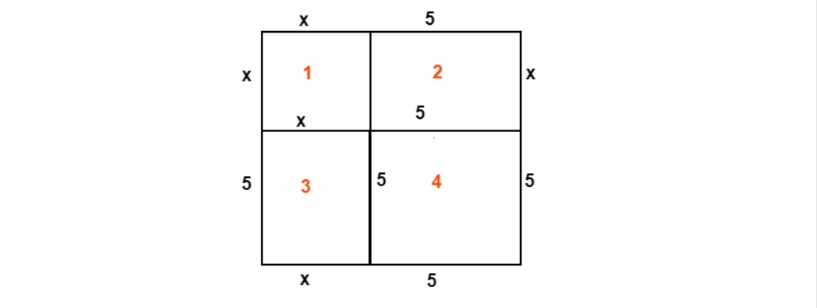
completing a square geometrically by adding a square

So, the whole area of square #1, the rectangle #2 and rectangle #3 is equal to 39 m² as we evaluated in the beginning.

The area of square #4 is equal to 5 x 5=25 .

The area of the whole shape (large complete square) is equal to:

(x + 5)² = 25 + 39

(x + 5)² = 64

Let’s find x from the equation (where x > 0, since this is a side length):

x + 5 = 8

x = 3

Therefore, the side length of the first room is 3 m.

So, using geometry, logic and the newly discovered algebraic symbols, Al-Khwarizmi could solve one of the most challenging problems of his time.

Completing a Square Using Algebra

Completing a square geometrically is still used to this day to visually demonstrate the process and explain why it is even called “completing a square” – well, because we literally complete the square by adding a missing square piece to an existing quadratic geometric formation.

In modern mathematics, though, an algebraic method is mostly used to solve problems like the one above, as well as problems involving any maximum or minimum quantities – converting the standard form of a quadratic equation into its vertex form. The vertex form of a quadratic equation provides the max/min value, as well as the value at which max/min value occurs.

For example, let’s consider the following problem:

A football is kicked into the air. Its height h, in meters, after t seconds is given by the
equation

$h=-4.9t^{2}+24.5t+1$