Congratulations! You are in your last year of high school and you want it to be a successful year. If you are planning to continue studying in a post-secondary institution, one of the grade 12 math courses is usually a requirement and you, no doubt, would want to ace grade 12 math.
No matter what grade 12 math course you are taking, there is a set of skills and knowledge that will definitely help you succeed.
Reducing Fractions
Knowing how to reduce fractions will help you get the correct answer and prevent you from losing marks for not expressing your answer in the simplest form.
Not every fraction can be simplified, but when it is possible, it is important to do so for clarity. To reduce a fraction, follow these steps:
1. **Identify the Numerator and Denominator**: The numerator is the top number of the fraction, while the denominator is the bottom number.
2. **Find the Greatest Common Factor (GCF)**: The GCF is the largest whole number that divides both the numerator and the denominator without leaving a remainder. To find the GCF, list the factors of each number and identify the largest one they share.
3. **Divide Both Parts by the GCF**: Once you have determined the GCF, divide both the numerator and the denominator by this number.
4. **Record the Resulting Fraction**: The fraction you get after dividing both the numerator and the denominator is the reduced form of the original fraction.
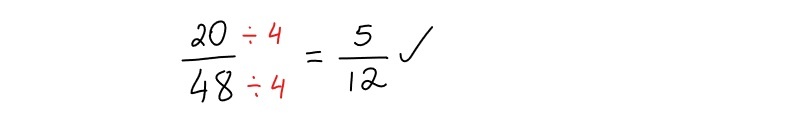
Simplifying Radicals
Another important skill in grade 12 that will most definitely help you earn better grades is simplifying radicals and rationalizing a denominator.
At times, when we encounter a value under a square root, we may find that it is not a perfect square. A perfect square is a number that can be expressed as the product of an integer multiplied by itself (for example, 1, 4, 9, 16, etc.).
When the value under the square root is not a perfect square, it cannot produce an integer when you take the square root. In these situations, it’s important to keep the non-perfect square value under the square root sign to maintain an exact answer. If you were to input this value into a calculator to obtain a decimal approximation, the result would lose its exactness, as decimals are inherently approximations.
However, there is usually a method to simplify the expression. We can often factor the value under the square root into two components: one that is a perfect square and another that is not. By isolating the perfect square, we can take its square root, resulting in an integer. This process allows us to express the square root in a simplified form, making it easier to work with while preserving the integrity of the original mathematical expression.
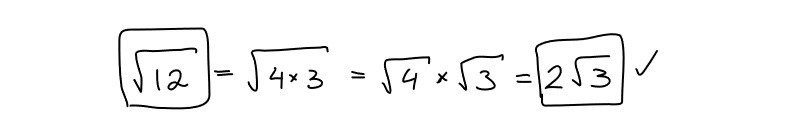
It is equally important to remember to rationalize the denominator when the denominator is a radical. When it comes to trigonometric ratios, the ratios for special angles are frequently determined in their exact form, containing a radical. Therefore, knowing how to rationalize the denominator will help ensure that you do not loose marks here and there for not expressing your solutions in the simplest form.
In order to rationalize a denominator that is just one value under the square root, for example, all you have to do is multiply both the denominator and the numerator by that same value under the square root. That will result in an integer in the denominator.
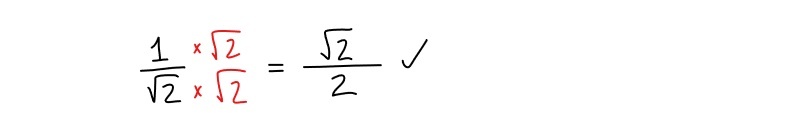
If the denominator is an expression containing a radical, then both the denominator and the numerator need to be multiplied by the conjugate pair of that expression (an expression with the opposite sign).
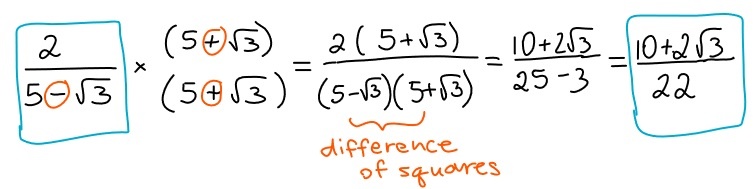
Factoring Quadratic Expressions
Mastering the concepts of common factoring, as well as factoring simple and complex trinomials, is fundamental for anyone looking to succeed in grade 12 math.
Additionally, it is important to be able to identify special factoring cases, such as the difference of squares and perfect square trinomials.
Common factoring involves extracting the greatest common factor from a polynomial, simplifying it for easier manipulation. Simple trinomials have the form ax² + bx + c, where a, b, and c are constants, and can typically be factored into two binomials.
Complex trinomials may require more advanced techniques and sometimes involve grouping or using the quadratic formula. Recognizing special cases is equally vital:
– **Difference of Squares**: This case applies when you have an expression in the form a² – b², which factors into (a + b)(a – b).
– **Perfect Square Trinomials**: These take the form a² ± 2ab + b² and can be factored into (a ± b)².
A strong grasp of these factoring techniques will not only improve your problem-solving skills but also help you excel in more advanced mathematical concepts.
Common factoring is the simplest form of factoring polynomial expressions. When factoring quadratic expressions, always look out to see if there is a common factor first, then proceed with other types of factoring where possible.
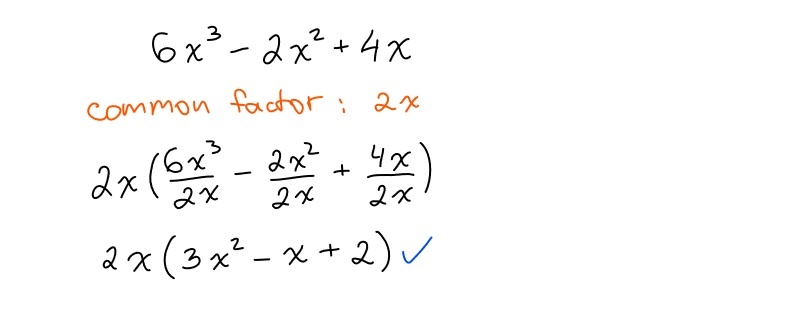
Factoring a simple trinomial means to factor a quadratic expression with the leading coefficient of 1, by finding the two numbers that multiply to equal the constant and add to equal the coefficient of the middle term in the expression.
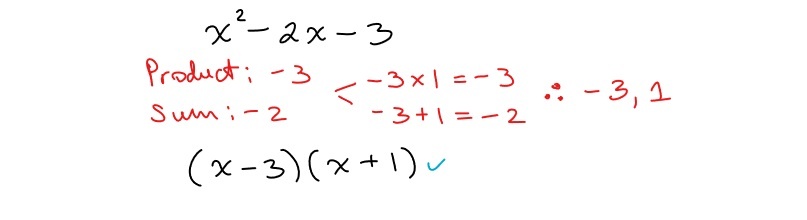
Factoring a complex trinomial means factoring a quadratic expression whose leading coefficient is not 1. In order to factor such trinomial it is necessary to decompose the middle term of the expression into two terms and then group two pairs of the resulting terms, common factoring at the end. Here is how
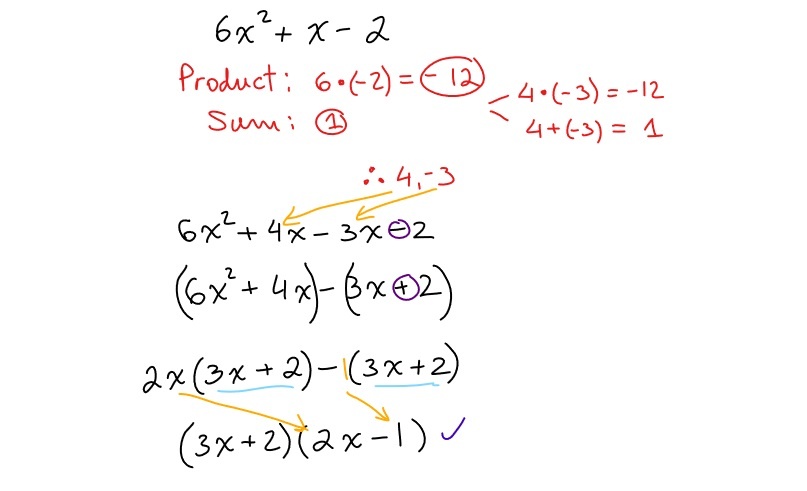
There are two special cases of factoring quadratics that frequently come up in grade 12 math in various situations (even when solving trigonometric equations or proving trig identities).
The first one is the difference of squares and here is an example
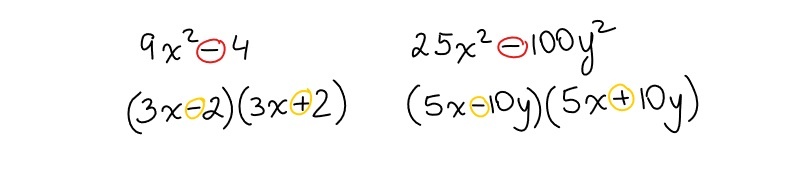
The second one is the perfect square trinomial and here is how to recognize it and factor it
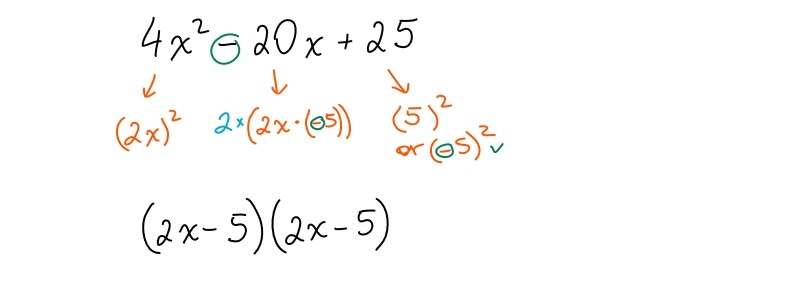
To excel in grade 12 math, there are several important factors to consider and practice. While the skills mentioned above are some of the most commonly used and easiest to review, it’s essential to focus on them to improve quickly.
So, don’t waste your time, make sure that your are proficient in the above and enjoy your grade 12 math success!
Here is the radicals practice
Here is the factoring practice
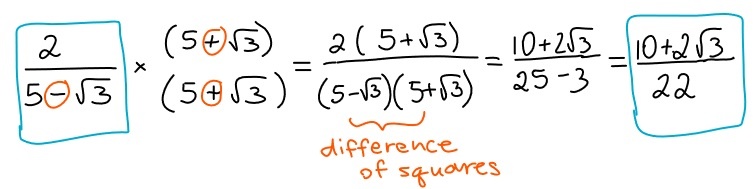
One thought on “Mastering Grade 12 Math: Your Path to Success”