Lesson 4: Multiplying and Dividing Fractions
Multiplying and dividing fractions is not complicated.
Knowing how to multiply and divide fractions will help you succeed when other, more complex mathematical concepts, such as simplifying algebraic expressions, solving equations and so on.
In order to multiply and divide fractions it is not required to find the GCF, unlike when adding and subtracting them.
Most students find the process of multiplying fractions the easiest of all operations with fractions. All you have to do is multiply numerators and denominators respectively (the product of the numerators over the product of the denominators), recording the final answer as a reduced simplest fraction. In order to reduce a fraction, divide both the numerator and the denominator by their GCF (greatest common factor).
The process of dividing the two fractions is a bit more complex. But as long as you understand why things are done a certain way everything is really simple.
In order to divide one fraction by another fraction, find the reciprocal of the second fraction and then change the operation to multiplication. To get the reciprocal of a fraction, just turn it upside down. Switch the numerator and denominator.
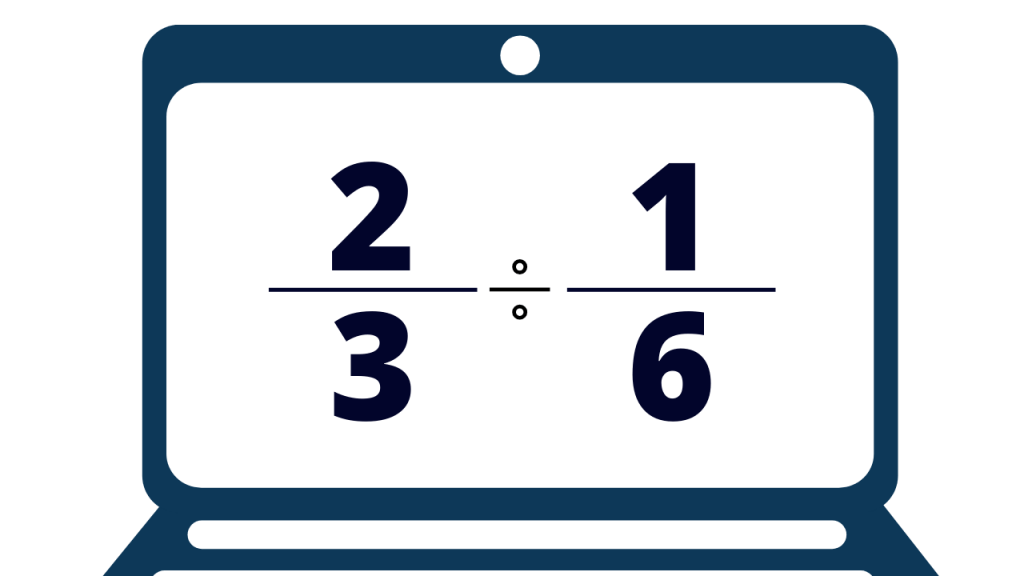
When you are required to multiply or divide mixed numbers, convert them into improper fractions first, then apply the rules discussed above. In order to convert a mixed number into an improper fraction, multiply the number of wholes by the denominator of the fractional part and add the numerator to the product. The result goes into the numerator. The denominator stays unchanged.
Multiplying and Dividing Fractions Quiz
