Lesson 6: Mixed Numbers
Improper fractions can be converted into mixed numbers (also called mixed fractions) by isolating the whole in the improper fraction.
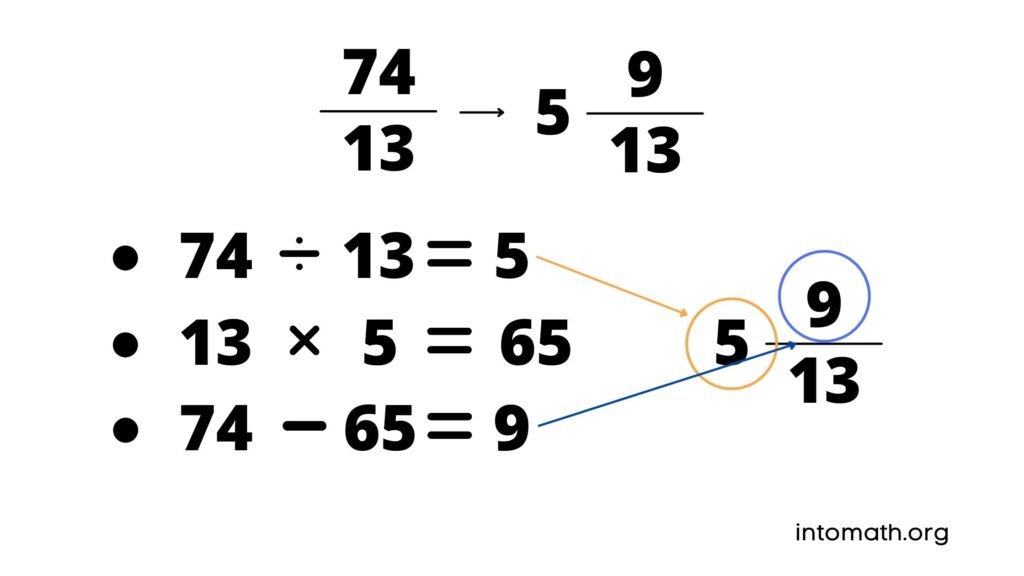
What is a Mixed Number?
A mixed number is a mathematical term that refers to the combination of a whole number and a proper fraction.
This representation is particularly useful when converting an improper fraction into a mixed number, as it allows for a clearer understanding of how many whole units are present along with any additional fractional part.
To visualize mixed numbers, one can think of them as consisting of whole units accompanied by portions of another unit. For example, in the short animation provided below, we illustrate the concept using pizzas, which effectively demonstrates how mixed numbers can be seen in everyday scenarios.
This visual representation is crucial, as it helps bridge the gap between the intuitive understanding of mixed numbers and their mathematical notation on paper or digital formats.
When it comes to performing arithmetic operations with mixed numbers, the process involves a systematic approach. We start by adding or subtracting the whole number components. Following this, we address the fractional parts. It is important to note that if the resulting sum of the fractions is an improper fraction, we must convert it into a mixed number to express it in a more understandable form.
Furthermore, when dealing with mixed numbers that contain fractions with different denominators, it is necessary to find equivalent fractions that share a common denominator. This step ensures that we can accurately add or subtract the fractions involved. In summary, mastering the representation and manipulation of mixed numbers enhances our overall mathematical problem-solving abilities and fosters a deeper comprehension of fractions in general.
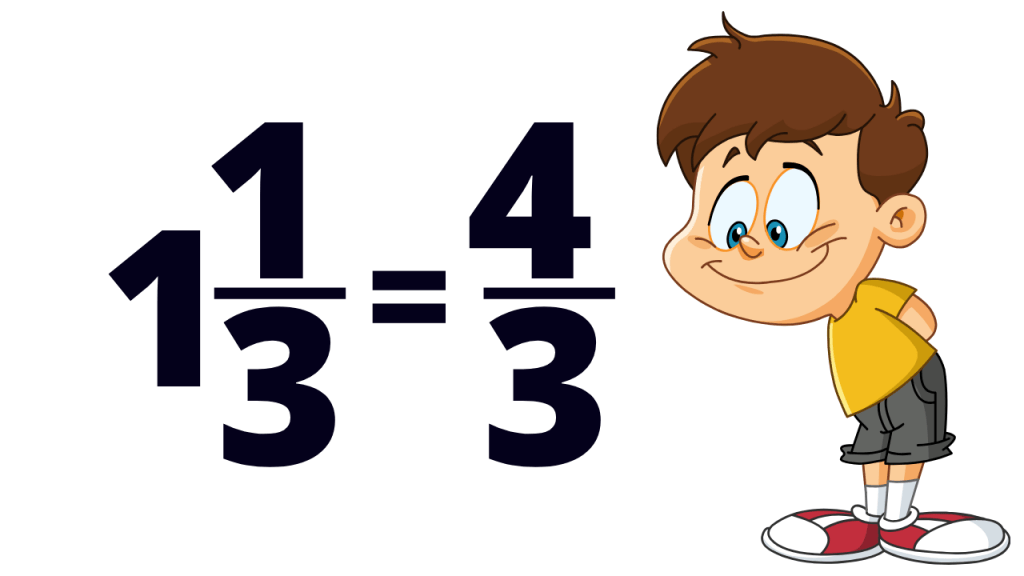
Writing Improper Fractions as Mixed Numbers
1. Divide the denominator into the numerator
2. The quotient is the whole number of the mixed number that goes in the front
3. The remainder goes into the numerator of the fractional part of the mixed number
4. If there is another number in the numerator already, add the remainder to it
5. The denominator of the fractional part stays the same